oblicz pole otrzymanych trapezów jolka: Proszę o pomoc,nie radzę sobie z geometrią.Trapez równoramienny o podstawie 4cm i 9cm oraz wysokości 16cm podzielono na dwa trapezy podobne prostą równoległą do podstawy. Oblicz pole otrzymanych trapezów.

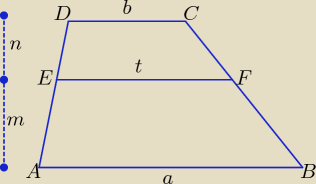
Bogdan: Odcinek EF równoległy do podstaw dowolnego trapezu (punkt E należy do ramienia AD, punkt F do ramienia BC) rozdziela trapez ABCD na dwa podobne trapezy ABFE i EFCD. Oznaczenia jak na rysunku.

a		t		m		m		√a
	=		=		⇒ t = √ab i		=
t		b		n		n		√b

	m		√a
skala podobieństwa trapezów : k =		=
	n		√b

PABFE		a
	= k2 =
PEFCD		b

W tym zadaniu: a = 9, b = 4, m + n = 16. t = √9*4 = 6

m		√9		m		3		3
	=		⇒		=		⇒ m =		n
n		√4		n		2		2

3		5
	n + n = 16 ⇒		n = 16 ⇒ n = 6,4 i m = 9,6
2		2

	1
PABFE =		(9 + 6)*9,6 = 72
	2

	1
PEFCD =		(6 + 4)*6,4 = 32
	2

	3		9
Sprawdzenie: k =		⇒ k2 =
	2		4

	9
PABFE = k2*PEFCD ⇒ 72 =		* 32 ⇒ 72 = 72.
	4