. asdf: pochodne mam taką pochodną: arctg(sin³[√x*(3x²+2)])^{ln cos2(x2*tg(2x))} jakbym napisał rozwiązanie byłby ktoś w stanie mi to sprawdzić? (bo jest tego trochę)

Ajtek: Cześć asdf . Sorry, ale na mnie nie licz, nie ten poziom

asdf: czesc, szkoda

Ajtek: Myślę, że ktoś łaskawy się znajdzie .

asdf: napisałbym rozwiązanie do sprawdzenia , ale tego jest tak duzo, ze na marne nie chce pisac

Ajtek: Wyobrażam sobie ile tego jest . Może napisz sam wynik .

asdf: ok, zaraz

asdf: czesciowo spróbuję jak narazie to napisać:

	x2*2x*ln2
ln (cos2(x2 * tg(2x)) ) ' = −2tg(x2*tg2x) * (2xtg2x +
	cos2(2x)

zrobisz to? ( porownamy wyniki)

Ajtek: asdf jescze do takich pochodnych nie doszedłem

asdf: aha To lipa z działań..

Ajtek: Chwila, coś pokombinuję .

asdf: ok

asdf: spróbowałem zrobić jeszcze raz tą pochodną (z 19:59) i wyszło mi:

	x2*2x*ln2
−2tg(x2*tg(2x) * ( 2x*tg(2x) +		)
	cos2(2x)

Ajtek: asdf, poprosilem Milę w dwóch wątkach żeby zerkneła. Mam nadzieję że pomoże .

asdf: Ok, dzięki bardzo

asdf: Chcę obliczyć tą pochodną licząc po kolei jej części..

Joanna: na początku poch z arctg(WNĘTRZE)= ¹_{1+(WNĘTRZE)²}

	gf'
a potem to wymnożyć przez pochodną Wnętrza czyli ze wzroru f(x)g(x)= fg(g'lnf+		)
	f

niezła pochodna, Ty mate studiujesz?

Joanna: ok , policzyłam..jak już masz to ok, jak nie− odezwij się na 2057388, bo jak wiesz, szkoda tyle pisac daremnie

asdf: nie, samemu sobie daje takie zadania.

Ajtek: Wariat

asdf: pochodna tego:

	1
ln(cos2(x2*tg(2x)))' =		* [cos2(x2*tg(2x)))]' =
	cos2(x2*tg(2x)))

2cos(x2*tg(2x)) * ( cos(x2 * tg(2x)) )'
	=
cos2(x2*tg(2x))

−2cos(x2*tg(2x))*sin(x2*tg(2x)) * (x2*tg(2x))'
	=
cos2(x2*tg(2x))

−2*sin(x2*tg(2x)) * (x2*tg(2x))'
	=
cos(x2*tg(2x))

−2tg(x²*tg(2^x)) *[ (x²)' * tg(2^x) + x²*(tg(2^x))' ] =

	1
−2tg(x2*tg(2x)) *[ 2x * tg(2x) + x2*		* (2x)' ] =
	cos2(2x)

	1
−2tg(x2*tg(2x)) *[ 2x * tg(2x) + x2*		* (2x * ln2 ] =
	cos2(2x)

	x2*2x*ln2
−2tg(x2*tg(2x)) *[ 2x * tg(2x) +		]
	cos2(2x)

.

asdf: pochodna ln(cos²(x²*tg(2^x)))' =

	x2 * 2x * ln2
h'(x) = −2tg(x2*tg(2x)) *[ 2x * tg(2x) +		]
	cos2(2x)

pochodna ln(arctg(sin³(√x*(3x²+2)))' = g'(x) =

1
	*
arctg(sin3(√x*(3x2+2)))

3x2+2   3sin(√x*(3x2+2)) * cos(√x*(3x2+2)( + 6x√x)   2√x
sin6(√x(3x2+2))+1

więc całość: e^{h(x) * g(x)} *( h'(x)* g(x) + g'(x)*h(x) ) podstawiając do równania wyszło mi: e^{ln(cos2(x2*tg(2x)))* ln(arctg(sin3(√x*(3x2+2)))} *

	x2 * 2x * ln2
(−2tg(x2*tg(2x)) *[ 2x * tg(2x) +		] *
	cos2(2x)

	1
(ln(arctg(sin3(√x*(3x2+2)))) +		*
	arctg(sin3(√x*(3x2+2)))

3x2+2   3sin(√x*(3x2+2)) * cos(√x*(3x2+2)( + 6x√x)   2√x
	*
sin6(√x(3x2+2))+1

ln(cos²(x²*tg(2^x))) ] dobrze?

Mila: 20:49 dobrze.

asdf: (sin²(2x))^lnx ' = e^{lnx*ln(sin2(2x))} '=

	sin2(2x)
elnx*ln(sin2(2x)) * (		+ 4sin(2x)*cos(2x) * lnx) =
	x

	sin2(2x)
elnx*ln(sin2(2x)) * (		+ 2sin4x * lnx) =
	x

Joanna: wg Ciebie do jakeij potęgi jest podniesiony sin (2x) ?

asdf: @Mila dzięki, druga pochodna źle policzona, jutro wrzucę, sprawdzisz?

mmmmmmon: Pomocy please Uprość wyrażenie: 27(2m – 1) – (2m – 3)2 – (7m + 2)(7m – 2) + 8m2, a następnie oblicz jego wartość dla m = 2 + 1.

Ajtek: Mila

asdf:

	x
arctg		> arctg(−1)
	x+2

x ∊ R /{0}

x
	> − 1
x+2

2x + 2
	> 0
x+2

2(x+1)(x+2) > 0 x∊ (−2;−1)

Mila: Zacznij liczy normalne zadania.

jikA: Złe dałeś założenie bo dla x = −2 (należy do Twojego założenia) zobacz co dostajesz.

asdf:

	x+3
arcctg(		) > arcctg(−1)
	x

D: x ∊ R/{0}

x+3
	< −1
x

2x+3
	< 0
x

	3
2x(x+		) < 0
	2

	3
x ∊ (−		;0)
	2

asdf: tamto zadanie jest totalnie źle, znam juz odp. wiec pomine prawidlowe.

Mila: które jest źle?, już nie wiem co chcesz?

asdf: 22:05 jest źle, pochodna ln(arctg(sin³(√x*(3x²+2))) też jest źle jak coś.

Ajtek: asdf, chciałeś żebym sprawdzał Twoje, a zerknij do mnie i zobacz z czym ja sie kopie .

asdf: dziedzina:

arcsin(x+2)
arccos(x + ln(x−2))

dziedzina: −1 ≤ x+2 ≤ 1 arccos(x+ln(x−2)) ≠ 0 −1 ≤ x + ln(x−2) ≤ 1 x − 2 > 0 i to do kupy i jest

asdf: @Ajtek ok

Mila:

	x
y=arctg(		)
	x+2

	x		−π
arctg(		)>
	x+2		4

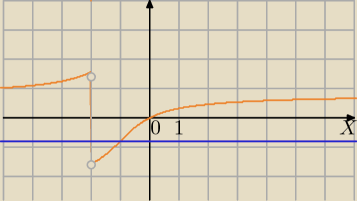
odczytaj i popraw swoje zadanie z 22:05

asdf: x ≠ −2 x ∊ (−∞;−2)u(−1;∞)

Joanna: ^{arcsin((1₂)x}_√2−ln(x)

Joanna: licznik arcsin(2^x) mianowink √−1−ln(x+3)

asdf: ta pochodna jest dobrze policzona?:

	1
ln(arctg(sin3(√x * (3x2 + 2))) ' =		*
	arctg(sin3(√x(3x2+2)))

arctg(sin³(√x(3x²+2)))'=

1		1
	*		* sin3(√x(3x2+2)))' =
arctg(sin3(√x(3x2+2)))		(sin6(√x(3x2+2))+1)

1		1
	*		* 3 sin2(√x(3x2+2))) *
arctg(sin3(√x(3x2+2)))		(sin6(√x(3x2+2))+1)

(sin(√x(3x²+2)' = 3sin²(√x(3x²+2))*cos(√x(3x²+2))*(√x'(3x²+2)+(3x²+2)'(√x)

	1
*		=
	arctg(sin3(√x(3x2+2))+1)

3sin²(√x(3x²+2))*cos(√x(3x²+2))*(U{3x²+2}{2√x)+ 6x^3/2) *

	1
	arctg(sin3(√x(3x2+2))+1)