Witam, łatwe, proszę o pomoc Mafi: Witam, proszę o pomoc 1. Oblicz wysokość ostr. praw. czworokątnego, którego krawędź podstawy ma dł. 6 i ściana boczna jest nachylona do podstawy pod kątem α=60*. 2. W ostrosłupie prawidłowym czworokątnym przekątna podstawy ma dł. 3√2, a wysokość równa się 8. Oblicz V tego ostr. Bardzo dziękuję za pomoc.

Kaja: narysuj sobie ten ostrosłup. ja nie wiem jak tu się rysuje figury przestrzenne. narysuj sobie też trójkąt w którym jedna przyprostokątną jest wysokość tego ostrosłupa (H), a druga jest równa połowie krawędzi podstawy czyli ma dł.3, zaś przeciwprostokątna to wysokość ściany bocznej ostrosłupa. wówczas można skorzystac z tangensa: tg60^o= ^H₃. i H=3√3

Mafi: nie musi być rysunek, wystarczy że podasz mi odp. to sprawdze z moimi i zobacze czy wszystko mam ok

Kaja: Zad.2. wzór na przekątną kwadratu to d=a√2, gdzie a to krawędź podstawy, zatem a√2=3√2,

	1
więc a=3. V=		*Pp*H
	3

	1
V=		*9*8=24
	3

Kaja: no to w pierwszym H=3√3, a w drugim V=24

Mafi: ok, tak właśnie mam dziękuję a to 1. zad ?

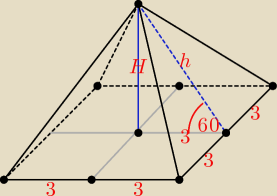
Bogdan: Rysunek do zadania 1. H = 3√3

Mafi: Dzięki wielkie: )

Bogdan:

	1
W zadaniu 2 można wykorzystać wzór na pole kwadratu: P =		d2, gdzie d to długość
	2

przekątnej kwadratu, nie trzeba wyznaczać długości boku kwadratu.

	1		1
W tym przypadku P =		*(3√2)2 = 9, Objętość V =		*8*9 = 24
	2		3

Mafi: Jeszcze jedno zadanko, jak można W ostr. praw. sześciokątnym krawędź boczna ma dł. 6 i jest 3 razy większa od krawędzi podstawy. Oblicz V i Pp tego ostrosłupa. Nie potrzeba rysunku, same dane

Kaja:

	4√3
podstawę mozna podzielić na sześć trójkątów równobocznych, więc jej pole to 6*		=6√3
	4

(krawędź podstawy to 2). potem policz wysokość ostrosłupa (z odpowiedniego trójkąta). powinno wyjść 4√2. V=8√6

Mafi: i tak mi wyszło dobra, wyniki potwierdzone to w porządku

Kaja: co do pola powierzchni to oblicz sobie pole jednej ścianki bocznej. skorzystaj z trójkąta w którym jedna przyprostokątna to wysokość ostrosłupa, druga to wysokość trójkąta równobocznego o krawędzi 2 (tego w podstawie ostrosłupa). jak wyjdzie wysokość, to policz pole powierzchni bocznej. dodaj pole boczne do pola podstawy i już

Kaja: aha, to Pp to pewnie było pole podstawy, a nie pole całkowite no ale ważne że wyszło

Mafi: i mamy Pc= Pp + Pb= 6√3 + 6 √35 ?