Funkcja kwadratowa z parametrem matt: Dana funkcja f(x)=x²+kx+3 ma co najmniej jedno miejsce zerowe. dla jakich wartości parametru k miejsca zerowe tej funkcji należą do przedziału (−2;1)? proszę o pomoc, ponieważ nie chce mi wyjść. Zrobiłam założenia delta>= 0 f(−2)>0 f(1)>0 i −b/2a>0 ale po wyciągnięciu części wspólnej wyszedł zbiór pusty co jest błędną odp. Bardzo proszę o pomoc

matt: tam ma być −b/2a należy do przedziału(−2;1) moja pomyłka, przepraszam. Czy ma ktoś pomysł na to zadanie

pigor: ... warunki masz dobre : zobaczmy więc co mi wyjdzie Δ = k²−12 ≥0 i −2<−^k₂< 1 /*(−2) i 4−2k+3 >0 i 1+k+3 >0 ⇔ ⇔ |k| ≥2√2 i 4 > k >−2 i k< 3,5 i k >−4 ⇔ ⇔ (k≤−2√2 lub k ≥2√2) i −2< k <3,5 ⇔ 2√2 ≤ k <3,5 ⇔ ⇔ k∊<2√2; ⁷₂) . ...

matt: źle przepisałem funkcję, w treści jest f(x)=x²+2kx+3 . Mam prosbę pigor czy mógłbyś/mogłabyś teraz sprawdzić. Bo liczyłem 2 sposobami i za kazdym razem wychodzi zbiór pusty. Przepraszam za tą pomyłkę

Kaja: to w końcu miejsca zerowe mają należeć do tego przedziału czy −b/2a? poza tym to chyba ta nierówność wynikająca z delty nie jest dobrze rozwiązana, powinna być suma przedziałów (−∞,−2√3) i (2√3,+∞)

matt: przepraszam za wszelkie pomyłki, oto poprawna treść: Dana funkcja f(x)=x2+2kx+3 ma co najmniej jedno miejsce zerowe. Dla jakich wartości parametru k miejsca zerowe tej funkcji należą do przedziału (−2;1)? CO DO PYTANIA KAI: wydaje mi się że skoro msc−a zerowe mają należeć do przedziału (−2;1) to wierzchołek równiez musi należeć do tego przedziału...

Kaja: tak masz rację, ale mnie nie o to chodziło. teraz już wszystko jasne

Mat: wierzcholek z pewnoscia należy do przedzialu −2,1 ... skąd wzieliscie −b/2a>0 ? a moze −b/2a>−2 i −b/2a<1 ...

matt: Mat poprawiłem to już, ale nadal wychodzi zbiór pusty

Mat: no to napisz po kolei co wychodzi z delty itd.

Kaja: mnie wyszło (−2,−√3>∪<√3,⁷₄). sprawdź czy taka ma być odpowiedź

Mat: czesc wspolna ke(2,1)

Mat: z delty : −oo, − sqrt 3 u sqrt3 , + oo z wierzchołka : k e (2,1) f(−2)>0 k<7/4 f(1)>0 k>−3/2

matt: sęk w tym że nie mam odp wiem tylko, że zbiór pusty jest źle. : z delty mi wyszło k należy(−niesk, −{3}) suma({3};+niesk) . Kaja czy mogłabyś mi podac swoje założenia/ sposób obliczeń

Kaja: zakładamy, że Δ>=0 i f(−2)>0 i f(1)>0. Δ=(2k)²−4*1*3=4k²−12 4k²−12>=0 k²−3>=0 (k−√3)(k+√3)>=0 k∊(−∞,−√3>∪<√3,+∞) f(−2)>0 (−2)²−4k+3>0

	7
k<
	4

f(1)>0 1+2k+3>0 k>−2 no i część wspólna tego wszystkiego to ten przedział, który napisałam

Mat: kaja ma źle

matt: z wierzchołka:k należy(−1;2) f(−2)>0 i f(1)>0 − wychodzi mi zbiór pusty

Mat: widze że nie dasz se przetłumaczyc

Kaja: co do wierzchołka, to wydaje mi się że założenie jest niepotrzebne, ale nawet jakbyś to założył, to i tak część wspólna byłaby taka sama ( z tego założenia odnośnie wierzchołka byłoby, że k∊(−2,4))

Kaja: ah wzięłam do wierzchołka to co było na początku, więc to nie przedział (−2,4)

Kaja: no ale z Mat się nie zgodzę, jak cos to już przedział (−1,2)

Mat: nie umiesz liczyć i widać od razu że pojęcia nie masz o tym co mowisz... p>−2 i p<1 założenie konieczne. macie rozwiazanie to sie teraz głowcie , a nie sie spieracie

Mat: ! i k>−3/2 ! z f(1 !)

Kaja: Mat do kogo to piszesz?

pigor: ... a mnie wychodzi po zmianie równania : k∊<√3;⁷₄) .... bardzo mały przedział . ...

Mat: do Ciebie zobacz jak obliczylas

Kaja: jesli taki jesteś mądry to napisz jaki przedział będzie rozwiązaniem

Mat: napisane macie wyżej.lol >>>> (2,1)

matt: do mata−−−> czego nie dam sobie przetłumaczyc chyba mi wyszło, napiszę moje wyniki: z delty k należy(−∞;{3}>∪,{3};+∞) f(−2)>0 k należy (−∞;7/4) f(1)>0 k nalezy (−2;+∞) z wierzchołka: k nalezy (−1;2) z tego część wspólna wychodzi <{3};7/4) i co myślicie

Kaja: pigor a nie powinno tam byc jeszcze (−2,−√3>?

Mat: matt − źle

matt: mat: dlaczego

Mat: z delty : −oo, − sqrt 3 u sqrt3 , + oo z wierzchołka : k e (2,1) f(−2)>0 k<7/4 f(1)>0 k>−3/2

matt: chodzi o ten wierzchołek

Mati_gg9225535: ja sie zgadzam z Kaja

Mat: aa widze już ... z wierzchołka mamy [przedzial (1,2) . i najdz czesc wpolna tego wszystkiego i tyle

matt: f(1)>0 1+2k+3>0 4+2k>0 2k>−4−−−>k>−2

Kaja: Mat ty chyba źle liczysz skąd ci wyszło , że f(1)>0 dla k>−3/2 ?

Kaja: matt dobrze policzył

pigor: ... nie może, bo jak jest k≤−√3 i −1< k<2 ⇒ k∊∅ , więc do wyrzucenia reszta w koniunkcji . ...

Kaja: niech Mat się najpierw nauczy liczyć a potem dyskutuje

Mati_gg9225535: −√3 < −√4 −√3 < −2 czyli (−2, −√3>

Kaja: pigor tylko czemu mamy robic założenie odnośnie wierzchołka? po co to?

matt: z wierchołka mamy: −2k/2>−2 i −2k/2<1 −k>−2 i −k<1 k<2 i k>−1 k nalezy (−1;2) to moje obliczenia, co ma źle

pigor: ... , wierzchołek jest ważny bo cała parabola musi siedzieć między −2 i 1 . ...

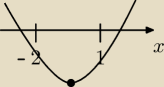
Mati_gg9225535: Kaja ma racje, jesli wierzchoilek bedzie nalezal do tego przedzialu to miejsca zerowe niekoniecznie...

Mati_gg9225535: wierzchołek*

Kaja: tak , zgodzę się z pigorem. zrobiłam obliczenia dla −1,8 i niestety miejsce zerowe wyszło powyżej 1. Więc rozwiązanie pigora jest poprawne

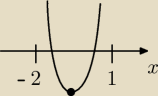
Mati_gg9225535: a musimy miec cos takiego

pigor: oczywiście wierzchołek w koniunkcji z warunkami f(−2) >0 i f(1)>0 zapomniałem dodać . ...

Kaja: założenie odnośnie wierzchołka faktycznie jest konieczne

Mati_gg9225535: wydaje mi sie ze jesli warunki na miejsca zerowe beda ok f(−2) >0 i f(1)>0 to wierzcholek automatycznie powinien siedziec pomiedzy ?

matt: dziekuję wszystkim za odpowiedzi bardzo mi pomogliście

Mati_gg9225535: a juz widze, faktycznie

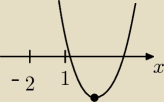
Mati_gg9225535: f (−2>0 i f(1) > 0 spelnione a wierzcholek swoja droga

Kaja: tak jest. bardzo dobry przykład

matt: mam jeszcze jedno zad do sprawdzenia: suma dwóch liczb, ich iloczyn i różnica ich kwadratów są równe. Znajdź te liczby. a+b=a*b=a²−b² a+b=(a+b)(a−b)−−−−>stąd a−b=1 czyli a =b+1 b+1+b=(b+1)*b 2b+1=b²+b b²−b−1=0−−−−−−−>wyszło mi b=1−√5/2 lub 1+√5/2 zatem a=3−√5/2 lub a=3+{5}/2 w II przypadku gdy a+b=0 wówczas a+b=(a+b)(a−b) 0=0\ L=P czyli dla a=0 i b= 0 warunki zadania też sa spełnione. Odp. Szukane pary liczb to (3−√5/2,1−√5/2) lub (3+√5/2, 1+√5/2) lub (0,0) czy mógłby to ktoś spr chodzi mi głównie o to czy nie ma jeszcze jakichś opcji?

kasia: to są wszystkie