pomoc pilne!!! arne: proszę o pomoc w rozwiązaniu: zbadaj przebieg zmienności funkcji

	3x
f(x)=√(−14x2+16x+17) lub f(x)=
	x2+1

Aga1.: Nie wiem, czy jeszcze potrzebujesz, ale trochę policzę

	3x
f(x)=
	x2+1

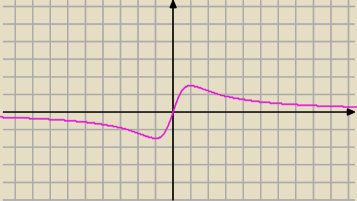
D=R więc nie ma asymptot pionowych

	3x		3x
limx→−∞		=limx→∞		=0
	x2+1		x2+1

Istnieje asymptota pozioma w + i − ∞ y=0 ( jeśli istnieje asymptota pozioma to nie liczymy ukośnej.) Teraz liczę pochodną tej funkcji

	3(x2+1)−2x*3x
f'(x)=
	(x2+1)2

Liczę miejsca zerowe pochodnej f^'(x)=0⇔3−3x²=0 x=1 v x=−1 −−−punkty podejrzane o ekstremum Monotoniczność funkcji f^'(x)>0dla x∊(−1,1) f↗ (−1,1) a maleje (−∞,−1),(1,∞)

	3
ymin=f(−1)=−
	2

	3
ymax=f(1)=
	2

Możesz liczyć drugą pochodną i określić punkty przegięcia i wypukłość.