granica funkcji liceum: Obliczyć granicę

	3x+6
limx→ −2
	x3+8

Wychodzi mi ³₄ a odpowiedź podana jest ¹₄

Eta: x³+8=(x+2)(x²−2x+4)

	3(x+2)		3
f(x)=		=
	(x+2)(x2−2x+4)		x2−2x+4

	3		1
lim x→ −2=f(−2)=		=
	12		4

liceum: o, zapomniałem że w tym wzorze na sześcian jest też minus dzięki

Eta:

liceum: Jeszcze jedna problematyczna:

	x2−x−2
limx→−1
	x2+1

Aga1.: Podstaw za x= −1 i oblicz wartość

asdf:

	0
jak masz symbol [		] i x → jakiegoś punktu, np. a to mianownik i licznik dzieli się przez
	0

(x−a)

pigor: ... podstaw x= −1 do funkcji podcałkowej i tyle , koniec , masz granicę .

liceum: nie czaję, po podstawieniu wychodzi lim_{x→ −1} ⁰₂

Aga1.:

	0
Ale tu nie ma
	0

Aga1.:

	0
A ile to jest		?
	2

asdf: ale ja nie napisałem, że jest...

liceum: teoretycznie 0, ale odpowiedź mam podaną −1 albo −4 (ręcznie napisana, nie jetem w stanie odczytać)

liceum: chyba że odpowiedź złą mam podaną...

Aga1.: A to może jest tak

	x2−x−2		(x+1)(x−2)
limx→−1		=lim x→−1		=
	x2−1		(x−1)(x+1)

	x−2		−3
limx→−1		=
	x−1		2

liceum: plus jest na bank, przykład jest drukowany, tylko odpowiedzi ręcznie dopisywane, dobra tam. ktoś się pomylił przy przepisywaniu

asdf: dla pocwiczenia zrób przykład Agi, jak Ci zalezy oczywiscie

liceum: dla pocwiczenia to ja mam milion innych xD i tak wszystko robie dodatkowo dobra, jeszcze jedno (tutaj to ja zapisu nie rozumiem)

	√1+cosx
limx→ π+0
	sinx

liceum: I jeszcze gdyby ktoś mógł sprawdzić :

	tgx		sinx   cosx		1
limx→0		=limx→0		=1*limx→0		=1*1=1 dobrze to jest?
	x		x		cosx

asdf: ale co to znaczy: x−>π⁺0? drugie jest dobrze

liceum: no wlasnie nie wiem co to znaczy

asdf: nie wiem, jak chcesz to moge Ci podeslac granice do zabawy, sa w miare czytelne, bez de'hospitala.

liceum: chetnie sie pobawie

liceum: w sumie juz rozumiem te prostsze (zrobiłem około 150 przykładów, to miałem problem w jakichś 3−4)

asdf: zanim wrzuce to masz juz przestawiony twoj przyklad, chyba o takie cos chodzilo;

	√1−cosx
limx−>0
	sinx

asdf: tu bedziesz miec jednostronne, (jak miales to rob, jak nie to odpusc)

liceum: nie mialem, ale wszystko sie przyda

asdf: proszę, troche pobazgrane bo jakos trzeba sobie radzić.. http://www15.speedyshare.com/rqguu/download/granice-funkcji.jpg

	a
To jak bedziesz liczyc granice i bedziesz mieć symbol [		]; a ∊ R to nie rób tych
	0

przykładów, ale granice jednostronne "może" na pierwszy rzut oka są trudne, ale to tylko złudzenie

asdf: no to jeżeli chodzi o ten przykład:

	0		√(1−cosx)(1+cosx)
limx−>0 U{√1−cosx{sinx} = [		] = limx−>0		=
	0		sinx(√1+cosx)

	√1−cos2x		√sin2x
limx−>0		= limx−>0		=
	sinx(√1+cosx)		sinx(√1+cosx)

	| sinx |		0
limx−>0		= [		]..dalej jest ten symbol, a wartosci
	sinx(√1+cosx)		0

bezwzględnej "ot tak" nie mozna sobie skracac, dlatego liczy sie granice jednostronne (cokolwiek to znaczy na razie): z lewej strony liczby dążące do zera, zapisuje się w taki sposób: x−>0⁻ z lewej strony liczby dążące do zera, zapisuje się w taki sposób: x−>0⁺

	|sinx|
limx−>0+		= wartosc bezwzgledna bedzie dodatnia, bo argument
	sinx(√1+cosx)

dążący do zera z prawej strony przyjmuje wartości dodatnie.

	sinx		1		1
limx−>0+		=		=
	sinx(√1+cosx)		√1+1		√2

argumenty sinusa dażące do zera z lewej strony przyjmuja wartosci ujemne, czyli w tym przypadku wartość bezwzgledna z liczby ujemnej, np. |x| dla x < 0 = −x, czyli w duzym skrocie bedzie:

	−sinx		−1		−1
limx−>0−		= limx−>0−		=
	sinx(√1+cosx)		√1+1)		√2

asdf: poprawiam: z prawej strony liczby dążące do zera, zapisuje się w taki sposób: x−>0⁺

liceum: dzieki, na razie zostawie te rozwiazanie , jutro poczytam o tych jednostronnych (mam to na swojej kartce o granicach ) i sprobuje zrozumiec, dzieki wielkie za rozwiazanie i za zadania

asdf: powodzenia

liceum: coś takiego :

	x2+3x−2		2
limx→ 1		=		i jaki wniosek z tego?
	x3−3x+2		0

Aga1.: Licz granice: lewostronną i prawostronną i jeśli są równe to istnieje granica w 1 i równa się granicom jednostronnym

liceum: to sobie ominę na razie

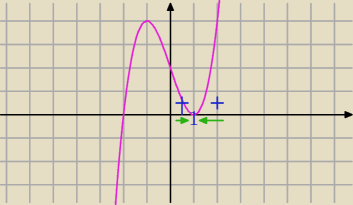
Aga1.: Narysowałam wykres mianownika

	x2+3x−2		2
limx→1−		=[		]=∞
	x3−3x+2		0+

	x2+3x−2		2
limx→1+		=[		]=∞
	x3−3x+2		0+

Jaka jest granica Twojej funkcji przy x→1?

liceum: ∞

Aga1.: Ok.