wyznaczyc równanie prostej jacek: jak wyznaczyć równanie prostej. mając 4 punkty w 3d np A(3,2,1) B(4,5,6) itd. nie umiem znaleźć zadnej podpowiedzi do mojego zadania w internecie

Nienor: Z 4 punktami na upartego da się rozwiązać układ: Ax+By+Cz+D=0 i wyznaczyć A,B,C,D. Ale równanie prostej można policzyć już chyba z dwóch punktów.

jacek: okej, jeżeli mamy już to Ax+By+Cz+D=0 to co pod co mam podstawić? przy równaniu płaszczyzny, liczyłem wektor AB x AC, macierz wyliczyłem, z i, j, k wyszedł jakis tam wynik, liczby, które były przy i, j,k podstawiłem pod wzór: A(x−x₀)+B(y−y₀)+C(z−y₀)+D=0 liczby te podstawiłem pod A, B, C licząc D, ale nie wiem co podstawic pod, x,y, z ? w zadaniach na zajęciach był zawsze podany jakis punkt i x,y,z brało sie z tego punktu, a teraz go nie ma podanego i nie wiem o co chodzi.

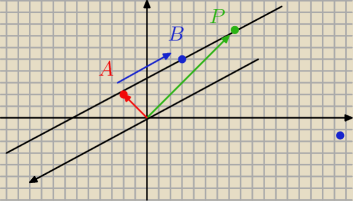
Nienor: Ale ty mówisz mam 4 punkty i chcę wyznaczyć równanie, a nie, że je masz. Nie wiem o co ci chodzi. O szybszą niż podstawianie metodę? Jeżeli A i B leżą na prostej k, a punkt O jest początkiem układu współrzędnych, a P jest dowolnym punktem leżącym na tej prostej, to równanie prostej k wygląda tak: OA+tAB=PO, gdzie t ∊ℛ

jacek: moja dokładna treeść zadania. Dane są punkty A(3, 2, 1), B(1, 2, 4), C(1, 3, 1), D(−2, −3, 7). g) wyznaczyć równanie prostej nie rozumiem, niestety tego całego wykresu i tego pod nim równania

jacek:

Nienor: To najprostszym sposobem będzie, jak pisałam wyliczenie tego z układu równań. Wektor OA+t*AB będzie zawsze dla danego punktu równy OP [3,2,1]+t[−2,0,3]=[x,y,z] − postać wektorowa prostej x=3−2t y=2 z=1+3t − postać parametryczna prostej

jacek: dziekuje bardzo, łatwe rozwiazanie jak się je jakoś ogarnia w końcu mam nadzieję, że na kolokwium prowadzacy uzna taki sposób liczenia, bo takiego nie pokazywał, a każde inne mi tu nie pasuje.