Geometria analityczna. Okąg i styczna. Równanie. V.Abel: Cześć! Szukam pomocy w zadaniu : Napisz równanie okręgu przechodzącego przez punkt (1,0) i stycznego do prostych y= −x−3 oraz y=−x+2. policzyłem ze wzoru na odległość odcinka średnicę okręgu, no to mam promień. wiem, że proste są równoległe, ale ... CO MI TO DAJE? jak znaleźć środki ? bo okręgi będą dwa, tak czuję.. POMOCY !

Mila: Czy masz odpowiedź?

V.Abel: tak, są dwa okręgi o S₁(−0,75, 0,25) oraz S₂(1,25 , −1,75) czy jakoś tak, nie mam tego przy sobie teraz, ale chciałbym wiedzieć jak z tym dalej walczyć

Mila: Tak mi wyszło, jeszcze podaj promien, bo te rachunki brzydkie, wolę skonsultować.

V.Abel: 25/8 w kwadracie prawdopodobnie, mi tak wyszło, chyba tyle było, wiem, że coś paskowało, tylko środka nie miałem. Jak to ugryźć?

V.Abel: pasowało* pardon

V.Abel: pasowało * pardon

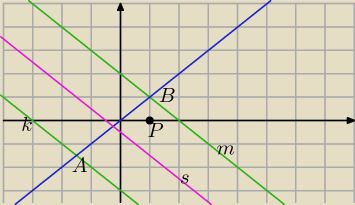
Mila: n: prostopadła do m i k , przechodząca prze Q=(0,0) y=x Wsp. A i B

	−3		−3
A: y=x i y=−x−3⇔A=(		;		)
	2		2

B: y=x i y=−x+2 ⇔B=(1;1)

	−1		−1
Srodek AB: S=(		;		)
	4		4

środek okręgu stycznego do k i m leży na prostej równoległej i przechodzącej przez S

	−1		1		1
s: y=−x+b oraz		=		+b⇔b=−
	4		4		2

	1
s:y=−x−
	2

	1		1		5√2
O(a;−a−		) współrzędne środka okręgu; r=		AB=
	2		2		4

	1		25
(x−a)2+(y+a+		)2=		i P−(1;0)∊okręgu
	2		8

	1		25
(1−a)2+(a+		)2=
	2		8

	15
2a2−a−		=0
	8

Δ=16

	1−4		−3		5
a1=		=		lub a2=
	4		4		4

	−3		1		1		5		1		−7
b1=−(		)−		=		lub b2=−		−		=
	4		2		4		4		2		4

V.Abel: Ok, a dlaczego ten środek leży na prostej równoległej, znaczy się zawsze tak jest, że środek leży na prostej równoległej?

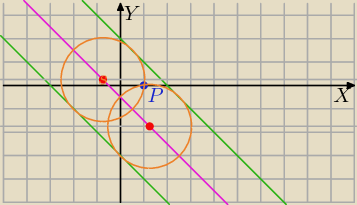
Mila: Pomyśl. 1)Środek okręgu musi być jednakowo odległy od obu prostych. 2) Jeżeli proste będą się przecinać, to środek okręgu stycznego do prostych będzie leżał na dwusiecznej kąta między prostymi, bo dwusieczna jest zbiorem punktów jednakowo odległych od obu ramion kąta

V.Abel: Ok, dzięki czyli środek leży na prostej równoległej, bo musi być równoodległy, tak jest zawsze przy stycznych ? P.S. Dzięki wielkie za pomoc

Mila:

V.Abel: Wracam jeszcze do tego tematu, bardzo proszę o odpowiedź, czy połowę odległości między tymi

	2+(−3)
prostymi równoległymi można wyliczyć też z tego:		w sensie, że wyszło, tylko czy
	2

to jest "dozwolone" ? . .

Mila: Odległość mierzymy długością odcinka prostopadłego do obu prostych. AB⊥m i AB⊥k I co Ci wyszło? Przecież odległość nie może byc ujemna.

V.Abel: Mila, miałem na myśli nie długość odcinka, tylko prostą równoległą do stycznych, która

	2+(−3)
przechodzi przez środek okręgu. No i w taki sposób		policzyłem współczynnik b z
	2

równania

	1
y=−x −		. Wyszło mi , tylko czy tak wolno liczyć? . .
	2

Mila: A to jest dobrze i bardzo sprytnie.Podoba mi się.

V.Abel: Ok, wiem, że dobrze, tylko jak to wytłumaczyć, bo zrobiłem, wyszło, ale dlaczego tak można, uzasadnienie?

Mila: S jest środkiem symetrii odcinka AB

V.Abel: S jest środkiem odcinka AB, ok, ale jak wytłumaczyć to co zapisałem, bo to daje dobry wynik, ale może ktoś to mi "łopatologicznie" wyjaśnić, błagam ! ! !

Mila:

	1
Znalazłeś punkt na osi OY− (0; −		) taki, że jest środkiem odcinka RQ.
	2

R=(0;2) i Q=(0;−3), gdzie R i Q należą do prostych równoległych przechodzących przez te punkty.

	1
Prosta równoległa do obu prostych i przechodząca przez (0; −		) jest jednakowo odległa od
	2

nich. To jest oczywiste i nie masz powodu do takich dokładnych wyjaśnień.

	1
punkt (0; −		) jest jednakowo odległy od obu prostych,
	2

policz sobie.

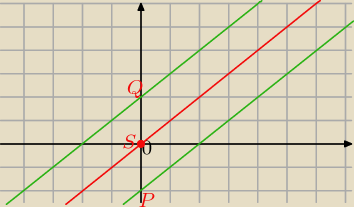
Mila: (0+0):2=0 (−2+2):2=0 S=(0;0)

V.Abel: Ok! dobra, dzięki, racja, dzięki za cierpliwość

Mila: