oblicz odleglosc cieciwy CD od srodka kola. XYZ. :P: Pole kola jest rowne 72¹₄πcm². Cieciwa CD przecina srednice AB w punkcie E, odleglym o 5cm od srodka kola. wiedzac, ze pole trojkata EBD jest 9 razy wieksze od pola trojkata ACE, oblicz odleglosc cieciwy CD od srodka kola.

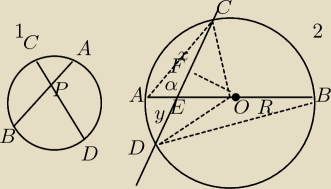
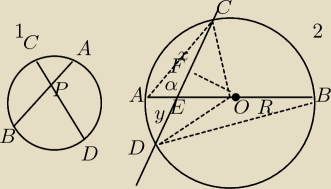AS: Rozwiązanie zadania opiera się na twierdzeniu: Jeżeli dwie cięciwy okręgu AB i CD przecinają się wewnątrz okręgu w punkcie P to iloczyn powstałych odcinków jest stały (Rys.1) PA*PB = PC*PD W zadaniu naszym wiemy że: (Rys.2) P = 72*π , OE = 5 , PΔEBD = 9*PΔACE , znaleźć FO 1. Z pola koła znajdziemy promień koła P =π*R² ⇒ 72*π = π*R² ⇒ R² = 72 = 36*2 ⇒ R = 6*√2 2. EB = R + 5 , AE = R − 5 Z twierdzenia wcześniej podanego mamy: CE*ED = BE*AE ⇒ x*y = (R + 5)*(R − 5) ⇒ x*y = R² − 5² ⇒ x*y = 72 − 25 x*y = 47 [1] 3 PΔ BED = 1/2*BE*ED*sin(α ) = 1/2*(R + 5)*y*sin(α) PΔ ACE = 1/2*AE*CE*sin(α) = 1/2*(R − 5)*x*sin(α) PΔ BED = 9*PΔ ACE 1/2*(R + 5)*y*sin(α) = 9*1/2*(R − 5)*x*sin(α) po uproszczeniu (R + 5)*y = 9*(R − 5)*x [2] Z [1] wyliczam y; y = 47/x wstawiam do [2] (R + 5)*47/x = 9*(R − 5)*x ⇒ (R + 5)*47 = 9*(R − 5)*x² (R + 5)*47 (R+ 5)*47 R + 5 (R + 5)²*47 x² = −−−−−−−−−− = −−−−−−−−−− * −−−−−−−−− = −−−−−−−−−− 9*(R − 5) 9*(R − 5) R + 5 9*(R² − 5²) (R + 5)²*47 (R + 5)² R + 5 x² = −−−−−−−−−−− = −−−−−−− ⇒ x = −−−− 9*47 9 3 4. Mając x znajdujemy y = 47/x = 47*3/(R + 5) = 141/(R + 5) 5. Szukam odległości cięciwy CD od środka okręgu CF = (x + y)/2 Z tw. Pitagorasa CO² = CF² + FO² FO² = CO² − CF² Na dokończenie nie mam już czasu.