oblicz CD XYZ. :P: Na przedluzeniu przeciwprostokatnej AB trojkata prostokatnego ABC obrano punkt D tak, ze BD=BC. oblicz CD, jesli wiadomo, ze BC=15cm i AC=8cm.

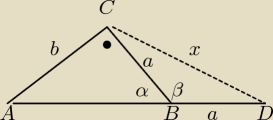
AS: Dane: BC = BD = a = 15 cm , AC = b = 8 cm , Szukane: CD = x 1. Z tw.Pitagorasa wylicz AB (z ΔABC − powinno być 17 cm). 2. β = 180^o − α 3. W ΔDBC zastosuj tw.cosinusów Powinno być: x² = 2*a² − 2*a²*cos(β) 4. cos(β) = cos(180^o − α) = −cos(α) 5. x² = 2*a² + 2*a²*cos(α) po wstawieniu 4 do 3 6. cos(α) = 15/17 z ΔABC Podstaw do piątej linijki i wylicz x − wynik końcowy x = 120/√17

XYZ. :P: A ile wynosi Cosβ i α? bo nie umiem tego podstawic, zeby wyszly calkowite liczby...

AS: cos(β) nie jest potrzebny do wyliczeń. Natomiast cos(α) wyliczamy z trójkąta prostokątnego ABC cos(α) = CB/AB = 15/17 (punkt 6)

XYZ. :P: to i tak nie wychodzi 120/√17, gdyby cos wynosil 16/17 to by wyszlo, ale tak to nie wychodzi mi

Bogdan:

	15		120
Sprawdziłem, zadanie jest poprawnie rozwiązane przez Asa, cosα =		, x =
	17		√17

AS: Rozpoczynam od 5 wiersza x² = 2*a²(1 + cos(α)) = 2*15²*(1 + 15/17) = 2*225*(17/17 + 15/17) x² = 450*32/17 = 9*2*25*16*2/17 = 4*9*16*25 Pierwiastkuję stronami x = 2*3*4*5/√17 = 120/√17

AS: W ostatnim x² poprawka,winno być x² = 4*9*16*25/17

fgdfg: ββββ