' Andzia: Dla jakich wartości parametru m równanie mx²+2x+m−2=0 ma dwa pierwiastki mniejsze od 1? Dziedzinę wyznaczyłam: m∊(1−√2,1+√2) i teraz skorzystałam z warunku x1<1 x2<1 czyli: (x1−1)(x2−1)>0 po przemnożeniu: x1x2 −(x1+x2)+1>0 z Viete'a

m−2		−2
	− (		) +1>0
m		m

z tego wychodzi 2>0 czyli R.... a powinno wyjść chyba m>0 bo w rozwiązaniach jest m∊(0,1+√2) Proszę o pomoc

Artur_z_miasta_Neptuna: ten warunek to za mało

Artur_z_miasta_Neptuna: x₁−1)*(x₂−1) > 0 ⋀ x₁+x₂ < 1+1

Andzia: Mogłabym Cię prosić o wyjaśnienie skąd ten warunek ? x1+x2 < 1+1

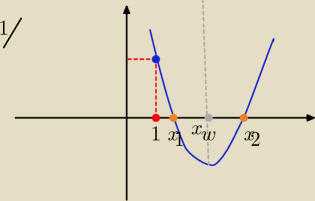
zombi: ja bym próbował takie warunki, żeby były mniejsze od jeden f(1)≠0 oraz x_w<1

Artur_z_miasta_Neptuna: x₁<1 x₂<1 i sumujesz te nierówności stronami i wychodzi x₁+x₂ < 1+1

zombi: źle ci powiedziałem, czekaj muszę to dorobić.

Artur_z_miasta_Neptuna: x₁<1 x₂<1 i sumujesz te nierówności stronami i wychodzi x₁+x₂ < 1+1 zombi a jak x_wierzchołka <1 zapewnić to, aby oba miejsca zerowe były <1

zombi: czekaj, bo widziałem kiedyś inaczej to zrobione, daj mi chwilkę...

zombi: da się tak jak ci mówiłem tylko musisz dodać tak x_w<1 1^o dla m<0 f(1)<0 2^o dla m>0 f(1)>0

Andzia: Arturze, ale dlaczego to sumujemy? I jak zsumować gdy w innym zadaniu będą przeciwne znaki, np jedno mniejsze a drugie większe?

Artur_z_miasta_Neptuna: Andziu ... ponieważ ... (x₁−1)*(x₂−1) > 0 jest spełnione gdy x₁ i x₂ <1 ... lub ... gdy x₁ i x₂ >1 i aby pozbyć się tej drugiej możliwości ... musisz zrobić, ze x₁+x₂ < 1+1

Eta:

	−b
1/ dla m >0 , Δ>0 , xw=		>1 i f(1)>0
	2a

2/ dla m<0 Δ>0 x_w>1 i f(1) <0

Eta: O kurcze przeczytałam dwa większe od 1 ( sorry)

Eta: Popraw , będzie tak jak podaje zombi

Andzia: Dziękuję wszystkim już rozumiem o co chodzi, spróbuję teraz rozwiązać sposobem Zombi i Ety