wartosc bezwzgledna maganda: lxl+lyl≤1

MQ: Bardzo ładna nierówność. W czym problem?

Saizou : lyl≤1−lxl y≤1−lxl i y≥lxl−1 zatem y∊<−1:1> i x∊<−1:1> czy jakoś tak

maganda: nierównosc trzeba rozpisac na przypadki czy zrobic na siatke znaczków

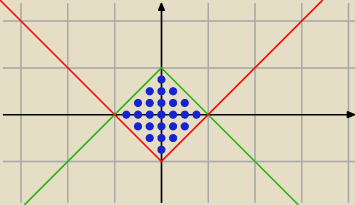
PW: A jakie było polecenie? Bo Saizou zrobił co można − zarówno ilustrację geometryczną jaki i udzielił odpowiedzi zielono−czerwonej. Możesz co najwyżej brnąć dalej: y−1≤−|x|∧y+1≥|x| −y+1≥|x|∧y+1≥|x| (y−1≤x≤−y+1)∧(−y−1≤x≤y+1) y−1≤x∧x≤−y+1∧−y−1≤x∧x≤y+1 (1) y≤x+1∧y≤−x+1∧y≥−x−1∧y≥x−1 Rozwiązanie nierówności składa się z wszystkich par (x,y) spełniających układ nierówności (1). Mnie osobiście więcej mówi rysunek niż te cztery nierówności (patrzę i widzę od razu, a układ nierówności nie jest taki czytelny).

maganda: y≤x+1∧y≤−x+1∧y≥−x−1∧y≥x−1\ Dziękuje, chodziło mi dosłownie o ta jedna linijkę