równanie trygonometryczne jaryn93: Rozwiąż równanie:

	π		π		1
sin(x+		)sin(x−		)=−		w przedziale <0,2π>
	3		3		2

Próbowałem to rozwiązać, ale nic mi nie wyszło

camus: Podpowiedź:

	cos(a−b)−cos(a+b)
sina * sinb =
	2

jaryn93: Tego wzoru nie ma w tablicach... Można to zrobić za pomocą wzorów z tablic, albo jakoś wyprowadzić ten wzór?

pigor: ... np. tak : z tablicowego wzoru na sinα*sinβ= ... ... ⇔ ¹₂ (cos²₃π − cos2x)= −¹₂ ⇔ cos²₃π − cos2x= −1 ⇔ ⇔ −¹₂ − cos2x= −1 ⇔ cos2x= ¹₂ i x∊<0,2π}> i narysuj sobie

pigor: w dobrych tablicach jest na pewno (np. tablice Cewe − niebieskie)

camus: Po pierwsze cos2x=¹₂=cos ^π₃ stąd 2x=^π₃ //i to bez tablic Po drugie, tego wzoru pigorze, wg. jaryna, nie ma w tablicach, więc trzeba znaleść inną metodę. Pozostaję jeszcze wzór na sinus sumy kątów, ale to by była męczarnia.

jaryn93: Chodziło mi o te maturalne... No nic wykuję ten wzór na pamięć

jaryn93:

	π		11π
odpowiedź to x=		v x=		tak?
	6		12

jaryn93: właśnie próbowałem wzorem na sumę kątów, ale chyba coś pomieszałem bo stanąłem na sin²x=2...

camus: Brawo. Zapomniałem, że cos ⁵₃ π = 0.

jaryn93: Mam drugie zadanie.. jak mogę naszkicować wykres funkcji f(x)=|log₂|x||?

jaryn93: Nie wiem za bardzo co zrobić z tą wartością bezwzględną z "x"

camus: 1)Narysuj log₂ x 2)Odbij to co po prawej stronie na lewą − dostaniesz log₂ |x| 3)Odbij to co poniżej osi X, nad oś X − dostaniesz |log₂ |x||

krystek: odbijasz sym względem osi OY prawą częśc wykresyu (dla x≥0)

jaryn93: odbijam prawą część na lewą? a nie odwrotnie?

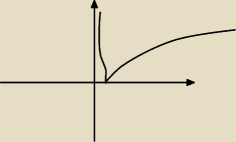
jaryn93: wyszło mi coś takiego, mniej więcej bo ciężko się tu rysuje dobrze?

jaryn93:

	5π
W równaniu trygonometrycznym coś wyszło źle. Powinny wyjść dodatkowo 2 rozwiązania,
	6

	7π
oraz		. Wytłumaczy ktoś dlaczego?
	6