znaleźć przedziały monotoniczności i ekstrema lokalne funkcji pomocy: Potrzebuje pomocyy ratunku wiem co trzeba w tym zrobic, ale na tym przykładzie sie totalnie pogubiłam:( znaleźć przedziały monotoniczności i ekstrema lokalne funkcji y=3x² −x−lnx

Artur_z_miasta_Neptuna: to pokaż swoje obliczenia ... przyjrzymy im się

pomocy: mam problem juz z sama pochodna bo w sumie mi wychodzi cos takiego: y'=6x−1−1/x a powinno chyba byc: y'=6x²−x−1 no i z tego obliczam delte i x1,x2 tak? to wtedy x1=−1/3, a x2=1/2 i jak to dalej mam zrobic?

Artur z miasta Neptuna: Nie nie ... to co masz jest dobrze ... ale wspolny mianownik zrob i to co napisalas bedzie Twoim licznikiem

pomocy: czyli jaki bedzie mianownik? nie mam pojecia jak to zrobic:((

Aga1.:

	1
y'=6x−1−
	x

	6x2		x		1
y'=		−		−
	x		x		x

	6x2−x−1
y'=
	x

y^'=0,gdy 6x²−x−1=0

pomocy: dziekuje teraz z tego delte tak? x1 i x2? i jak dalej? bo mi cos nie idzie:(

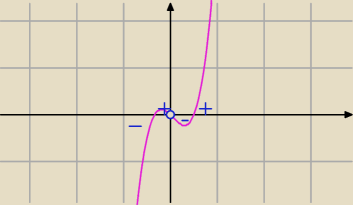
Aga1.: Miejsca zerowe pochodnej dobrze policzone i to są punkty podejrzane o ekstremum. Teraz rozwiąż nierówność y^'>0⇔x(6x²−x−1)>0 Oraz y^'<0 Na podstawie wykresu podaj odp.

pomocy: Tak wychodzi, że funkcja rośnie od (1/3; ∞)? w odpowiedziach mam, że mu wyjsc, ze rośnie w przedziale od (1/2;∞), a maleje w przedziale (0;1/2) tylko, że mi tak nie wychodzi

Aga1.: Trzeba pamiętać,że x>0. Rośnie tam, gdzie pochodna przyjmuje wartości dodatnie, czyli

	1		1
(		, ∞), a maleje, tam gdzie pochodna jest ujemna, czyli (0,		)
	2		2

	1		1		1
ymin=3*(		)2−		−ln		=
	2		2		2

pomocy: a jeszcze ostanie pytanie, ile wynosi ln1/2?

Aga1.: Tak zostaje, bo to jest liczba niewymierna

pomocy: a jeszcze asymtote z : 1/e^x−1 D: R/{0}? czyli nie ma asymptot pionowych? bo wychodzi 0. a jak z ukośna?

Aga1.:

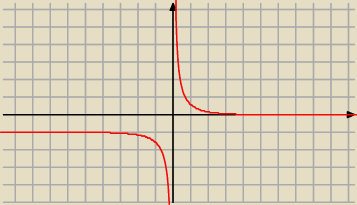
	1
f(x)=		, o takiej funkcji mowa?
	ex−1

pomocy: tak o takiej

Artur_z_miasta_Neptuna: no to widzisz na rysunku (16:20) że jest asymptota pionowa poziome (szczególny przypadek ukośnej) także są