prawdopodobienstwo SamsungA: Niech A i B oznaczają zdarzenia zawarte w przestrzeni zdarzeń elementarnych Ω. Wiadomo, że P(A')=0,37, P(B)=0,32, P(A−B)=0,43 . Oblicz P(A∩B) i P(A∪B). ps Co mi daje P(A−B)=0,43?, proszę o podpowiedź

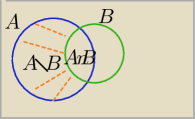
Eta: P(A\B)= P(A) − P(A∩B)

MQ: P(A−B)=P(A)−P(A∩B)

SamsungA: Wyszedł mi jakiś błąd, że P(A∪B) jest na minusie. Możecie jeszcze pokazać jak to policzyć albo pokazać same wyniki?

Bash: P(A')=0,37 więc P(A')=1−P(A) ⇒ P(A)=1−P(A'), podstawiając P(A)=1−0,37=0,63 P(A−B)=P(A)−P(A∩B) P(A∩B)=P(A)−P(A−B), podstawiając P(A∩B)=0,63−0,43=0,20 P(A∪B)=P(A)+P(B)−P(A∩B), podstawiając P(A∪B)=0,63+0,37−0,20=0,80

SamsungA: Dziękuje bardzo.