Proszę o pomoc Kamil1010: Zad. 6. Oblicz pole trójkąta ABC, wiedząc, że A(3,4), B(−1,−2), a wierzchołek C należy do prostej o równaniu 3x+4y−9=0. Zad. 7. Dane są punkty A(2,0), B(0,−4) oraz punkt C o pierwszej współrzędnej należący do prostej y=ax. Dla jakich wartości parametru "a" pole trójkąta ABC jest równe 10 Zad. 8. Napisz równania prostych w których zawierają się dwusieczne kątów wyznaczonych przez proste 2x+y−2=0 i x−2y−1=0. Zad. 9. Dany jest trójkąt ABC. Bok AB tego trójkąta zawiera się w prostej x−y=2, bok BC − w prostej y+2x=1, a bok AC − w prostej y−3x−6=0. Oblicz wysokość trójkąta ABC poprowadzoną z wierzchołka B.

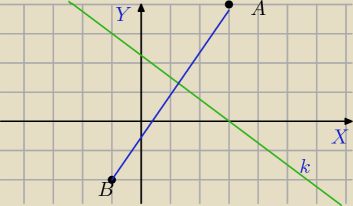
Mila: |AB|=√4²+6²=√52=2√13 6) 3x+4y−9=0. 4y=−3x+9

	−3		9
k: y=		x+
	4		4

	−3		9
C=(x;		x+		)
	4		4

Czy coś jeszcze wiadomo o ΔABC?

Kamil1010: nic więcej, tylko tyle mam w zadaniu