wymiary prostokąta wpisanego w półkole o promieniu R, którego pole jest najwięks aoshika: Wyznaczyć wymiary prostokąta wpisanego w półkole o promieniu R, którego pole jest największe. Rysunek nauczyciela w zadaniu wygląda tak http://www.bankfotek.pl/view/1401767 Bardzo bym prosił o pomoc w rozwiązaniu tego zadania.

Artur_z_miasta_Neptuna: pochodne były

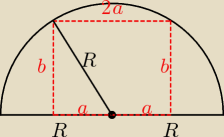
Artur_z_miasta_Neptuna: P_prostokąta = 2a*b gdzie: b = √R² − 4a² czyli: P_prostokąta = 2a*b = 2a√R²−4a² P'(a) = ....

aoshika: tak to jest w temacie z pochodnymi

Artur_z_miasta_Neptuna: to Ci już napisałem funkcję ... policz pochodną i wyznacz ekstremum

Artur_z_miasta_Neptuna: pamiętaj, ze 'a' to połowa dolnego boku

Artur_z_miasta_Neptuna: acha .. i jeszcze a∊(0,R)

aoshika: ok dzieki piwo

aoshika: hmm pochodna wychodzi 0 chyba ze cos zle robie a moze o to chodzi?

Artur_z_miasta_Neptuna: ja Ci dam 0

	1
P' = 2√R2 − 4a2 + 2a		*(−8a) = ... wspólny mianownik i redukujesz co się da
	2√R2−4a2

aoshika: ojoj kurcze dzięki naprawdę duże zimne piwo

lseaa: Dlaczego b=√R²−4a²? Nie powinno być raczej b=√R²−a²?