podobieństwo trójkątów ania96: W prostokącie ABCD punkt E jest środkiem boku BC. Odcinek DE przecina przekątną AC w punkcie F. Wykaż, że |AF|=2|FC| Z góry dziękuję za pomoc

pigor: .... z rysunku który sądzę już masz ΔCEF ≈ ΔADF (cecha kkk) , więc stąd i z warunków zadania :

|EC|		|AD|
	=		⇔ |AF||EC|= |AD||FC| ⇔
|FC|		|AF|

	2
⇔ |AF|*12|AD|= |AD||FC| /*		⇔ |AF|= 2|FC| c.n.w. . ...
	|AD|

pigor: ... cecha kkk, bo |∡FCE|= |∡FAD| − jako kąty naprzemianległe wewnętrzne , |∡EFC|= |∡AFD| − jako kąty wierzchołkowe , no to |∡FEC|= |∡FDA| − z tw. o sumie kątów Δ . ...

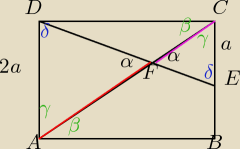
Aga1.: α− kąty wierzchołkowe są równe, β− kąty naprzemianległe sa równe γ=180⁰−(α+β) − suma kątów wewnętrznych w trójkącie wynosi 180⁰ Trójkąty AFD i ECF są podobne cecha podobieństwa trójkątów kkk.

	2a
Skala podobieństwa k=		=2.
	a

2		IAFI
	=
1		IFCI

Stąd IAFI=2IFCI

ania96: dziękuję bardzo