ze guess who: SZYBKIE ZADANKO, ZESPOLONE Na płaszczyźnie zespolonej narysować (wystarczy mi przekształcenie, nie trzeba wykresu) zbiory liczb zespolonych spełniających podane warunki:

	2
e) 0 < arg(sprzężenie{z}) ≤		π
	3

	2
Nie jestem pewny jak podejść do tego sprzężenia z "z". Czy wyjdzie 0 > arg(z) ≥		π? Mi
	3

tak wychodzi, ale widziałem inną odpowiedź i nie wiem skąd ona się wzięła. A no i jeszcze nie wiem jak do takiego podejść:

	π
0 < arg(z3) <
	2

Artur_z_miasta_Neptuna: czyżby ktoś wlasnie pisał kolo/egzamin

guess who: koło za 3 godziny, ale mam jeszcze mnóstwo materiału do powtórzenia i na tym się zatrzymałem

guess who: ej no ej! pomushcje!

guess who: z=r*e^iφ sprzężenie z "z" = r*e^−iφ , z tego co mi się wydaje. Czyli argument φ z liczby, w jej sprzężeniu daje −φ: arg(sprzężenie{z}) = −arg(z) ? Tak? A skoro tak, to podstawiając:

	2
0 < −arg(z) <		π /*(−1)
	3

	2
0 > arg(z) >		π
	3

2		4		3		1		π		π
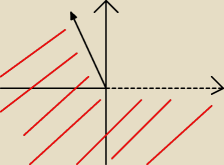
	π =		π =		π +		π =		+		, czyli wykres taki jak u góry?
3		6		6		6		2		6

Sławek: arg(z') = 2π − arg(z)

guess who: czyli ostatecznie wychodzi to samo, bo okres to 2π i jak podstawiając Twój wzór po przekształceniu będziemy mieli "0+2π", to robimy z tego po prostu "0"? I dalej dobrze zrobione? Czy jednak inaczej? No i ten drugi przykład,który podałem w pierwszym poście. Proszę chociaż o jakąś wskazówkę!

Godzio:

	π
arg(z3) <
	2

argz = φ

	π
0 < 3φ + 2kπ <		+ 2kπ
	2

	2		π		2
k *		π < φ <		+		π * k
	3		6		3

k = 0

	π
0 < φ <
	6

k = 1

2		5
	π < φ <		π
3		6

k = 2

4		3
	π < φ <		π
3		2

guess who: Dzięki wielkie!

guess who: Mam jeszcze jedną rzecz z zespolonych: z⁶ = (1−3i)¹² Powiedzcie jak to zacząć? Po prostu pierwiastkować dwustronnie, otrzymując "z = (1−3i)²"? Można tak? Czy prawą stronę przekształcić na trygonometryczną (co mi nie wychodzi − niestandardowe cos i sin)? Czy jeszcze jakoś inaczej?

guess who: Oczywiście chodzi o rozwiązanie tego równania

Godzio: To co zrobiłeś to będzie tylko jedno rozwiązanie ! Resztę otrzymujesz przez przesuwanie, zaraz rozpiszę.

guess who: Ech, znowu te kilka wyników, słaby ze mnie słuchacz na zajęciach, a Krystian z eTrapeza jakoś specjalnie nie zgłębiał się w tego typu przykłady. Dzięki z góry za rozpisanie!

Godzio: z⁶ = (1 − 3i)¹² z₁ = (1 − 3i)² = 1 − 6i − 9 = − 6i − 8

	π		π
z2 = z1(cos		+ isin		) = ...
	3		3

	π		π
z3 = z2(cos		+ isin		) = ...
	3		3

albo

	π		π		2π		2π
z3 = z1(cos		+ isin		)2 = z1(cos		+ isin		)
	3		3		3		3

z₄ = −z₁ z₅ = −z₂ z₆ = − z₃ (chyba tak ta końcówka)

	π		2π		π
A dlaczego kąt		? Ano dlatego że mamy z6 czyli		=		!
	3		6		3

Godzio: Jak jeszcze chcesz coś to pisz, bo za 15 min idę i sam zaczynam się uczyć na kolokwium

guess who: Dzięki. Skąd ja mam w tych zespolonych wiedzieć kiedy szukać kilku rozwiązań, a kiedy nie? :f Jednak w eTrapezie było coś podobnego, ale tylko przy pierwiastkach − znajdywało się jedno

	φ+2kπ		φ+2kπ
rozwiązanie i dalej z niego tym samym wzorem zk=zk−1(cos(		)+isin(		)).
	n		n

No, prawie tym samym, bo tutaj chyba nie ma tego φ? Kurde, muszę teraz to sam na jakimś przykładzie powoli przeanalizować.

Godzio: Zawsze masz szukać wszystkich rozwiązań jeżeli masz równanie zⁿ = coś to masz mieć n pierwiastków !

guess who: Dobra, czaję. Idę chyba zaraz na uczelnię i tam z kimś jeszcze rozwiążę kilka zadanek, gdybym czegoś jeszcze sam nie ogarnął. Dzięki za wszystko!

Godzio: Spoko, powodzenia !