zad Agnesssa: A jak można obliczyć e do potęgi jeden przez x ?

Mila: Podstawiaj za x liczby, i co konkretnie chcesz policzyć?

Agnesssa: Ogólnie to robię zadanie o treści: Wyznacz przedziały, w których funkcja jest malejąca i rosnąca f(x)=x²e do potęgi 1/x

Agnesssa: czy pochodna tej funkcji wynosi 2x*e do potęgi 1/x − e do potęgi 1/x ?

Mila: f(x)=x²e^1/x taka funkcja?

asdf: (x²*e^1/x)' = 2x * e^1/x − e^1/x

Agnesssa: tak, taka funkcja... czyli dobrze zrobiłam na tym etapie?

Radek: Chyba to będzie tak ale nie jestem pewien ((x²e)¹/x)'=(e¹/x(x²)¹/x(log(x²)−1))/x²

Mila: f(x)=x²e^1/x

	−1
f '(x)=2x*e1/x +x2*e1/x*(		)=2x*e1/x−e1/x
	x2

f '(x) =0⇔2x*e^1/x−e^1/x=0 e^1/x(2x−1)=0 2x=1

	1
x=		miejsce zerowe
	2

e^1/x(2x−1)>0⇔2x−1>0 (e^1/x>0 dl x≠0)

	1
x>		funkcja rosnąca
	2

	1
x<		i x≠0 funkcja malejąca
	2

	1		1		e2
dla x=		min lokalne f(		=
	2		2		4

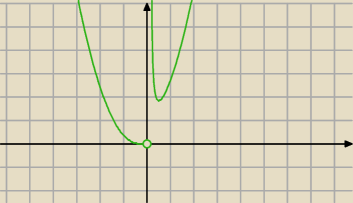
lim_x→0+(x²e^1/x)=∞ lim_x→0−(x²e^1/x)=0

Agnesssa: Dziękuję bardzo za rozwiązanie

Mila: