. asdf: oblicz:

	−1
arccos(		)
	2

jak sie za to wziąć?

SŁOŃCE POLSKIEJ MATEMATYKI: arccos(−1/2) = x ⇒ cosx = −1/2

asdf:

	−1
cos		= II lub III ćwiartka, czyli:
	2

	π
x =
	3

	2π		4π
x =		lub x =
	3		3

?

asdf: sorry, znalazłem taki wzór: arccos(−x) = π − arccos(x)

1
	= cosx
2

	π
x =
	3

arccos(−x) = π − arccos(x)

	1		π		5π
arccos(−		) = π −		=
	2		6		6

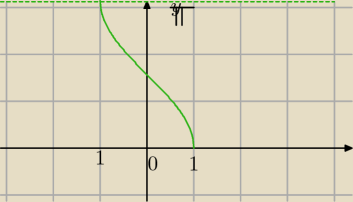Mila: y=arccosx, x∊<−1;1> y∊<0;π> arccos(−x)=π−arccosx

	−1		1		π		2
arccos(		)=π−arccos(		)=π−		=		π
	2		2		3		3

asdf: Dzięki, czyli mam dobrze (nie wiem czemu pozniej podstawilem pi/6). a jak wyznaczyc dzidzinę:

	x+1
arccos(		)
	x−2

	x+1
−1≤		≤ 1
	x−2

	x+1
−1≤
	x−2

x+1
	≥ −1
x−2

x+1
	+ 1 ≥ 0
x−2

x+1 + x − 2
	≥ 0
x−2

2x−1
	≥ 0
x−2

(2x−1)(x−2) ≥ 0

	1
(x−		)(x−2) ≥ 0
	2

	1
x∊ ( −∞;		>u<2;∞)
	2

teraz drugie równanie:

x+1
	≤ 1
x−2

x+1
	− 1 ≤ 0
x−2

x+1		x−2
	−		≤ 0
x−2		x−2

x+1 − x+2)
	≤ 0
x−2

3
	≤ 0
x−2

3(x−2) ≤ 0 x − 2 ≤ 0 x ≤ 2 x∊ (−∞;2> część wspólna:

	1
x∊ ( −∞;		>u<2;∞)u(−∞;2>
	2

	1
x∊ (−∞;		>u {2}
	2

asdf:

	1
i chyba zapomniałem dać x−2≠ 0 ⇒ x ∊ (−∞;		>
	2

asdf: ?

asdf: ?

asdf: jak takie coś policzyć?

	x+3
arcctg(		) > arcctg(−1)
	x

arcctgx jest funkcją malejącą, czyli powinna być zamiana znaku:

x+3
	< −1
x

x+3
	+ 1 < 0
x

x+3 + x
	< 0
x

2x + 3
	< 0
x

x(2x+3) < 0

	3
x(x +		) < 0
	2

	−3
x∊(		;0)
	2

a tu wolfram mówi inaczej http://www.wolframalpha.com/input/?i=arcctg%28+%28x%2B3%29%2Fx+%29+%3E+arcctg%28-1%29

asdf: ale tu arcctg, a nie tg.

ICSP: właśnie widzę xD Musiałbym pomyśleć

asdf: nom, jakbyś mógł

ICSP: jedyny pomysł jaki mam to zamienienie tego na arctg i dopiero później porównanie. Błędu u ciebie znaleźć nie mogę.

asdf: :( To jeżeli ja nie mam bledu, to przerobienie tego zmieni wynik? Jezeli zmieni wynik w takim razie ja mam blad albo drugie rozwiazanie jest błedem

ICSP: ty masz błąd tylko ja jestem za głupi aby go znaleźć. Zostajemy przy takiej wersji

asdf: ok

asdf:

x+3
	< −1
x

x
	> −1
x+3

x + x + 3
	> 0
x+3

2x +3
	> 0
x+3

(2x+3)(x+3) > 0 do tej postaci doszedłem...

asdf: a dziedzinę z postu 21 stycznia 00:13 mam dobrze?

asdf: .

asdf: ..