funkcje trygonometryczne pic:

	sinx
Rozwiąż równanie		= 0, x ∊ <−2π; 2π>
	cosx + 1

Na początek zapewne trzeba wyznaczyć dziedzinę, tak więc cosx + 1 ≠ 0 cosx + 1 ≠ 0 cosx ≠ −1 x ≠ π ⋀ x ≠ −π D: x ∊ <−2π; 2π> / {−π; π} Co dalej? Gdyby nie to "+1" w mianowniku to można by to zapisać jako tgx=0. Proszę o pomoc.

Ajtek: Ułamek jest równy 0 ⇔ licznik równy 0 sinx=0 i jedziesz.

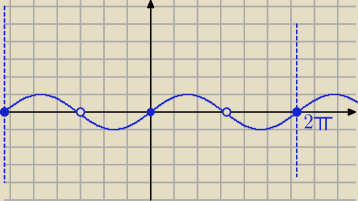Mila: sinx=0 i x∊D x=−2π lub x=0 lub x=2π