Znajdz pola pozostalych trojkatow asia: Przekatne trapezu rownoramiennego ABCD ,ktorego krotsza podstawa jest CD a pole wynosi P , przecinaja sie w punkcie S . Pole trojkata DSC wynosi 1/16P. Znajdz pola pozostalych 3 trojkatow , na ktore przekatne podzielily trapez. proszę o pomoc

Eta:

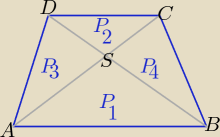
	1
k>0 skala podobieństwa trójkątów ABS i CDS P(ΔCDS)=P2=		P
	16

P₁=k²*P₂ , P₃=P₄=k*P₂ P(tr)= P₁+P₃+P₄+P₂ = k²*P₂+k*P₂+k*P₂+P₂= (k²+2k+1)*P₂ to: P= (k+1)²*P₂ ⇒ (k+1)²= 16 ⇒ k+1=4 ⇒ k=3

	9
P1= k2*P2=		P
	16

	3
P3=P4= k*P2=		P
	16

	3		3		1		9
Odp:		P,		P,		P,		P
	16		16		16		16

Eta:

	1
Dla jasności : P= (k+1)2*P2 ⇒ P=(k+1)2=		P ⇒ (k+1)2=16
	16

asia: wielkie dzięki ale mam 2 ale po pierwsze dlaczego P3=P4=k*P2, a nie P3=P4=k2*P2 ? tak by wynikało z P3/P2=k2 .... jesli moja wersja jest dobra to to zaburzy zadanie.... a po drugie P= (k+1)2*P2⇒ P=(k+1)2=1/16P.. ni bardzo wiem dlaczego z mnożenia P2 czyli 1/16 nagle jest znak = mimo wszystko jeszcze raz bardzo dziękuje

asia: ok to drugie ogarnęłam......ale o to pierwsze bardzo proszę o pomoc

Eta:

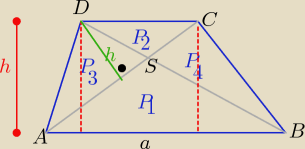
	a*h		a*h
P(ΔABD)=		= P1+P3 i P(ΔABC)=		= P1+P4
	2		2

to: P₁+P₃= P₁+P₄ ⇒ P₃=P₄

P1
	= k2⇒ P1= k2*P2
P2

|AS|= k*|SC|

	|AS|*h		|SC|*h
to: P3=		=		= P2 ⇒ P3= k*P2
	2		2

Michał558: |AS|= k*|SC| to: P3= |AS|*h/2=|SC|*h/2= P2 ⇒ P3= k*P2 sorki ale ja też jakoś chyba tego nie rozumiem