drzewko denatlu: 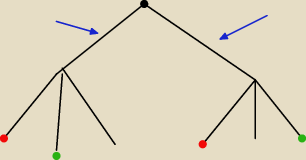CZy mógłby ktoś zerknąć czy to drzewko jest ok? Są dwa pojemniki z kulami. W jednym są 4 kule czerwone, 3 białe i 5 zielonych a w drugim 2 czerwone, 5 zielonych i 3 białe. Z każdego pojemnika losujemy po jednej kuli. Oblicz prawdopodobieństwo Zdarzenia A że wylosujemy dwie kule tego samego koloru Zdarzenia B że wylosujemy kulę czerwoną i zieloną Czy to drzewko jest ok? Bo tak narysowałem i wydaje mi się że złe, bo trzeba by coś w niebieskie strzałki, a przecież tam pasują tylko jedynki.

tn: Ja bym to zrobił tak, że: 6 krawędzi od korzenia: I pudełko: czerwona, zielona biała II pudełko: czerwna, zielona, biała Potem odpowiednio kolejny poziom.

Eta: Ja wolę takie

denatlu: tn: zaraz to przeanalizuje Eta: ale to moje to do bani ?

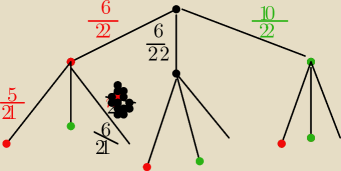
denatlu: tn: nie wiem jak to twoje ma wyglądać coś mi nie wychodzi, ale narysowałem coś takiego. Jest ok?

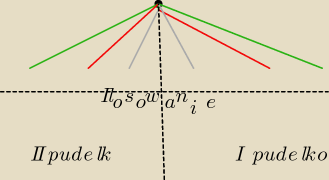
tn: Wg mnie.

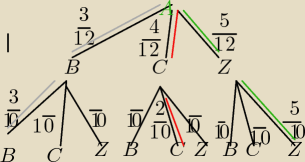
Mila: I pojemnik 4C,3B,5Z 12kul II pojemnik 2C,3B,5Z 10s kul A − wylosowano dwie kule w tym samym kolorze

	3		3		4		2		5		5		42		7
P(A)=		*		+		*		+		*		=		=
	12		10		12		10		12		10		120		20

tn: @Mila, a czemu ja źle podchodzę, bo zupełnie sobie sprawy nie zdaję ?

Mila: tn, wszystko przychodzi z czasem. Rozwiązuj zadania i sprawdzaj odpowiedzi.Czytaj rozwiązania w podręczniku. Rachunek prawdopodobieństwa jest trudny.Czytaj teorię.

tn: @Mila, dałbym chyba radę wyprowadzić te 6 krawędzi. Jak możliwe jest to, że radzisz sobie w ten sposób? Masz przecież dwa pudełka

Paulina: tn, Mila dobrze zrobiła. Pierwszy poziom, to losowanie z 1 pudełka a drugi z drugiego.

tn: A czemu nie na odwrót?

tn: Ponadto, też mogę to dobrze wykonać 6−oma krawędziami (tak mi się przynajmniej zdaje)

denatlu: no dzięki Mila.

Mila: TN, Możesz zacząć losować od II pudełka. Denatlu uzupełnij prawdopodobieństwa na gałązkach i oblicz z drzewka P(B)

tn: W urnie są 3 kule białe i 5 czerwonych. Losujemy trzy razy po jednej kuli. Co jest bardziej prawdopodobne: wylosowanie dwóch kul białych, jeśli losowanie odbywa się ze zwracaniem, czy jeśli losujemy bez zwracania? Zadanie polega na policzeniu dwóch prawdopodobieństw. Liczmy najpierw bez zwracania. Losuję trzy razy. Uwzględnię kolejność (ale postępuję głupio bo nie mam przekonania, skąd właściwie mam wiedzieć czy istotna jest kolejność?).

	8!
|Ω| =		= 6*7*8
	5!

A − zdarzenia polegające na wylosowaniu dwóch białych kul (jak nazwać to "porządnie" − nie zaznaczyłem, że losujemy trzy, z czego mają dwie być białe)

	3 2		5 1
|A| =		*		* 3! (mnożę razy trzy silnia, żeby uwzględnić kolejność)

	15*6		15
Więc P(A) =		=
	6*7*8		56

TERAZ ZE ZWRACANIEM B − zdarzenia polegające na wylosowaniu dwóch kul białych (również nie wiem jak to trafniej ująć − losuję przecież trzy, a nie tylko dwie ). |Ω| = 8³

	3 1		3 1		5 1
|B| =		*		*		* 3!

	3 1   3 1   5 1   * * * 3!		3*3*5 * 1 * 2 *3		135
P(B) =		=		=
	83		83		256

P(B) > P(A) czyli ze zwracaniem lepiej. Proszę o krytyczną ocenę tego co napisałem

Mila: Ja jutro,dziś już nie myślę.: Dobranoc