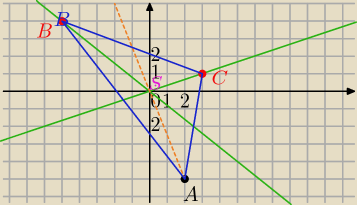
geometria analityczna ahu8: dane są dwie proste, które zawierają środkowe trójkąta: y=−4x/5 y=x/3 oraz punkt A=(2,−5) Wykonałam rysunek, punkt przecięcia prostych to S=(0,0) obliczyłam równanie prostej przechodzącej przez punkt A i S y=−5x/2 Muszę wyznaczyć pozostałe współrzędne trójkąta, ale nie wiem jak. Rysowanie koła wpisanego czy opisanego nic mi nie daje. A daje mi coś, że te proste są środkowymi trójkąta? Wychodzi na to, że punkt S to środek ciężkości... i co z tego?

ZK: Twierdzenie : Srodkowe trzech bokow trojkata przecinaja sie wjednynm punkcie zwanym srodkiem ciezkosci trojkata . Punkt ten dzieli kazda ze srodkowych w stosunku 2:1 tzn. odleglosc tego punktu od wierzcholka jest 2 razy wieksza od odlegolosci tego punktu od srodka przeciwleglego boku

ahu8: wspaniale, biorę się do roboty

T: ... i jeszcze to ... i układziki równań

ahu8: nie zrobiłam narobiłam sobie kupę niewiadomych...

Mila:

	4
y=−		x
	5

	1
y=		x oraz punkt A=(2,−5) B=(b1,b2); C=(c1;c2)
	3

I sposób Czy można z wektorami? II sposób

	4
Niech B leży na prostej y=−		x, to jego wsp.
	5

	4		1
B=(b1;−		b1), C=(c1;		c1)
	5		3

	a1+b1+c1		a2+b2+c2
wsółrzędne środka ciężkości:xs=		; ys=
	3		3

	a1+b1+c1		a2+b2+c2
S=(0;0)=(		;		)
	3		3

	2+b1+c1
⇔		=0
	3

4   1   −5+(− b1)+ c1   5   3
	=0
3

	4
b1=−5 to b2=−		*(−5)=4 i c1=3 to c2=1
	5

B=(−5;4) i C=(3;1)

Mila: ?

ahu8: czy to są wzory na współrzędne środka ciężkości w trójkącie?

Mila: Tak. Wyprowadzenie wzoru. http://www.zadania.info/8448802 wikipedia http://pl.wikipedia.org/wiki/Tr%C3%B3jk%C4%85t#.C5.9Arodek_ci.C4.99.C5.BCko.C5.9Bci

Mila: ?

ahu8: wreszcie zrozumiałam, zrobiłam, czuję się mądrzejsza o jeden wzór Ślicznie dziękuję za pomoc!

Mila: