Twierdzenie o odcinku łączącym środki dwóch boków trójkąta Aspa. : 1. W trójkącie ABC połączono środki boków i otrzymano w ten sposób trójkąt KLM. Wykaż, że: a) obwód trójkąta KLM jest dwa razy mniejszy od obwodu trójkąta ABC b) kąty trójkąta KLM mają takie same miary jak kąty trójkąta ABC. 2. W dowolnym trapezie ABCD, w którym AB||DC, poprowadzono przekątną DB. Niech punkty K, L, M oznaczają odpowiednie środki odcinków AB, DB, BC. Wykaż, że: a) punkty K, L, M są współliniowe b) długość odcinka KM jest średnią arytmetyczną długości podstaw tego trapezu. Bardzo proszę o opis rozwiązania!

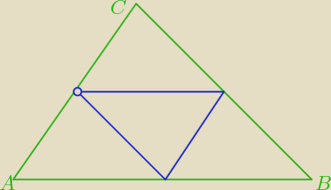
T: Ad.1 Cały czas Taleskiem − Jeśli podzielę odcinek AB na pół ... to tylko prosta przez ten środek a jednocześnie równoległa do AB podzieli BC na połowy. Skoro kąty są jednakowe ... to trójkąty przystające Skalę podobieństwa k wyznaczysz też z Talesa ... a skala podobieństwa wyznaczy stosunek obwodów −

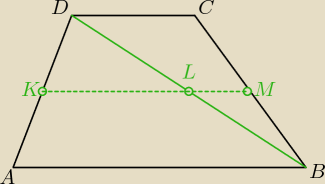
T: ... chyba masz tam literówkę w opisie A dowodzenie ... znów "Taleskiem" −

Aspa. : Nie do końca rozumiem to rozwiązanie, ale dziękuję.

T: posługując się trójkątami ABD , BCD wykażesz, że KL jest równoległa do AB LM jest równoległa do CD a skoro AB jest równoległa do CD to K, L, M muszą być współliniowe

LOL : α∫e że co? βo nie rozumiem 😂😂😂😂