Równoleglobok humanistka: Oblicz pole równoległoboku, w którym przekątne o dłuościach: 16 i 8 tworzą kąt 40stopni...

Eta: P= ¹₂ e*f*sinα e, f −−− przekątne α −−− kąt między nimi

Eta: sin 40^o −−−− odczytaj z tablic

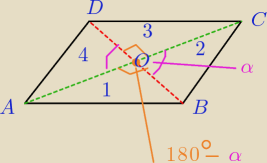
Eta: IACI= 16 => IAOI= 8 i ICOI= 8 IBDI= 8 => IBOI= 4 i IDOI=4 bo przekatne dzielą się na połowy pole1 ΔABO = pole 2 = pole3 = pole4 bo sin (180^o −α) = sinα więc P(równoległoboku) = 4*P_ΔAOD = 4*¹₂*¹₂*e*¹₂*f *sinα więc P(równoległoboku) = ¹₂*e*f*sinα teraz masz już udowodnione, że taki jest wzór na pole tego równoległoboku Podstawiaj i licz .... powodzenia!

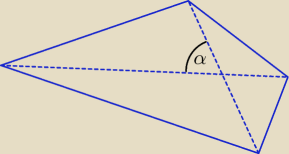
Bogdan: Dodam, że wzór P = ¹₂*e*f*sinα pozwala obliczyć pole powierzchni dowolnego czworokąta wypukłego, w którym e, f to długości przekątnych, α to miara kąta między przekątnymi.

Eta:

humanistka: Dziękuje Wam bardzo

sylwia gdańsk: swoja droga to dumnie nazwywac sie humanista

a: +→→→→→→→→