Oblicz pole P( tej części kwadratu gdzie jest strzałka).
hubal:
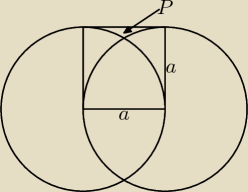
5 cze 18:18
hubal: proszę o pomoc
5 cze 18:20
hubal: dokładne polecenie do tego zadania
oblicz pola zakreskowanej figury, przyjmując dane podane na rysunku (tam gdzie jest strzałka
powinno być zakreskowane).
5 cze 18:29
Mariusz: pomagam

nie wiem czy to najłatwiejszy sposób ale taki mi przyszedł do głowy
5 cze 18:46
Eta:
Też jestem ciekawa ? ... czy wynik zgadza się z moim
 hubal
hubal ?...... masz jakąś odp?
5 cze 19:00
Mariusz:
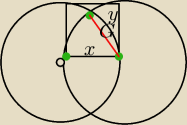
xy − używam nazw pól dużymi literami
X i Y to pola tych fragmentów w których sie znajdują litery
więc pole x i y równa się
X+Y=1/4πa
2
jeżeli w miejsce pola x wpiszemy trójkąt równoboczny to jego boki będą miały długość a
(wierzchołki trójkąta oznaczyłem kolorem zielonym). Pole tego trójkąta jest równe
G
pole X z wyłaćzeniem pola G jest równe X−G= 1/6 *πa
2 (1/6 bo kąt ma 60 stopni a to jest 1/6
pola koła) X=G+1/6*πa
2
| | a2√3 | |
czyli G=1/6*πa2− |
| (1/6 pola okręgu minus pole trójkąta)
|
| | 4 | |
| | a2√3 | |
czyli Y=1/4πa2−1/6πa2−1/6*πa2− |
| (Y=1/4 pola okręgu minus 1/6 pola minus G)
|
| | 4 | |
szukane pole P=1/4πa
2−Y i tylko wszystko podstawić i powyliczać
mam nadzieje że sie nigdzie nie pomyliłem, ale głównie chodzi o idee zadania

powodzenia
5 cze 19:08
Eta:
OK

Dodam ,że w zapisie: pole
koła , bo
okrąg nie ma pola

odp:
P= a2( 1 − π6 − √34)
P≈ 0,05a
2
5 cze 19:17
Mariusz: tak samo ci wyszło

(wzór) wim że okrąg ,

raz napisałem tak , raz tak

5 cze 19:18
Eta: 
OK
5 cze 19:20
Mariusz: to fajnie

5 cze 19:25
hubal: wielkie dzięki sam długo się nad tym męczyłem
5 cze 19:29
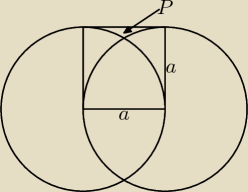
 nie wiem czy to najłatwiejszy sposób ale taki mi przyszedł do głowy
nie wiem czy to najłatwiejszy sposób ale taki mi przyszedł do głowy
 hubal ?...... masz jakąś odp?
hubal ?...... masz jakąś odp?
 xy − używam nazw pól dużymi literami
X i Y to pola tych fragmentów w których sie znajdują litery
więc pole x i y równa się
X+Y=1/4πa2
jeżeli w miejsce pola x wpiszemy trójkąt równoboczny to jego boki będą miały długość a
(wierzchołki trójkąta oznaczyłem kolorem zielonym). Pole tego trójkąta jest równe
xy − używam nazw pól dużymi literami
X i Y to pola tych fragmentów w których sie znajdują litery
więc pole x i y równa się
X+Y=1/4πa2
jeżeli w miejsce pola x wpiszemy trójkąt równoboczny to jego boki będą miały długość a
(wierzchołki trójkąta oznaczyłem kolorem zielonym). Pole tego trójkąta jest równe
 powodzenia
powodzenia
 (wzór) wim że okrąg ,
(wzór) wim że okrąg ,  raz napisałem tak , raz tak
raz napisałem tak , raz tak 
 OK
OK
