.
justyna: proszę o sprawdzenie
rozwiąż nierówność (x−3)≥1
x≥4 i (x−3)≤−1
x≤2
()− symbol wartości bezwzględnej
16 sty 23:10
asdf: wydaje mi sie, ze ta nierownosc ma dwa rozwiazania x−3 ≤ −1 x≤−2 lub 3−x≤−1 wiec x≥2
16 sty 23:16
justyna: dlaczego tak ?
16 sty 23:19
asdf: ponieważ istnieją dwie możliwości rozwiązań i dwie musisz podać, tak samo jest gdy na przykład
masz równanie x2 = 16 ,więc x = 4 LUB x=−4 to samo jest tutaj, kiedy opuszczasz wart
bezwzględną pojawiają Ci się dwie możliwosci (chyba, ze wart bezwzgledna wychodzi ujemna,
wtedy to jest sprzeczne)
16 sty 23:23
Saizou :
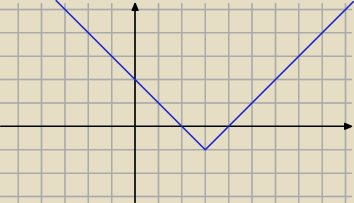
I sposób (graficznie)
lx−3l−1≥0
x∊(−∞:2> u <4:+∞)
II sposób
lx−3l≥1
x−3≥1 lub x−3≤−1
x≥4 lub x≤2
x∊(−∞:2> u <4:+∞)
16 sty 23:24
justyna: ja to musze jeszcze zaznaczyć na osi to wtedy jak ?
16 sty 23:24
Mila:
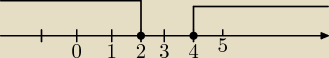
|x−3|≥1 odległość od liczby 3 jest większa lub równa 1 jedn.
x−3≥1 lub x−3≤−1⇔
x≥4 lub x≤2
16 sty 23:28
justyna: to juz w miare rozumiem ale mam jeszcze jeszcze jedno
−3 |2+x|≥9
16 sty 23:33
justyna: to musze wymnozyc to co w wartości bezwzględnej przez −3 ?
16 sty 23:34
Mila: Justyno, wartość bezwzględna jest nieujemna
|a|≥0 dla a∊R
|0|=0
|3|=3
|−5|=5 to jest odległość liczby od zera na osi liczbowej
−3|2+x|≥9⇔|2+x|≤−3 sprzeczność z definicją ( bo |2+x|≥0 i jest równa 0 tylko dla x=−2)
x∊Φ⇔brak rozwiązań.
16 sty 23:51
 I sposób (graficznie)
lx−3l−1≥0
x∊(−∞:2> u <4:+∞)
II sposób
lx−3l≥1
x−3≥1 lub x−3≤−1
x≥4 lub x≤2
x∊(−∞:2> u <4:+∞)
I sposób (graficznie)
lx−3l−1≥0
x∊(−∞:2> u <4:+∞)
II sposób
lx−3l≥1
x−3≥1 lub x−3≤−1
x≥4 lub x≤2
x∊(−∞:2> u <4:+∞)
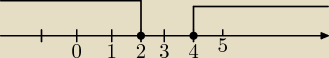 |x−3|≥1 odległość od liczby 3 jest większa lub równa 1 jedn.
x−3≥1 lub x−3≤−1⇔
x≥4 lub x≤2
|x−3|≥1 odległość od liczby 3 jest większa lub równa 1 jedn.
x−3≥1 lub x−3≤−1⇔
x≥4 lub x≤2