Eta:
więc tak :
najpierw zajmiemy się tym trójkątem ,by obliczyć jego boki
a, b, c −−− tworzą ciąg arytm.więc 2b= a + c
oraz a + b+c = 48
i a
2 +b
2 = c
2 −−− bo jest prostokątny
rozwiązując układ tych trzech równań :
2b + b = 48 => 3b = 48 =>
b= 16
to 2*16 = a +c i a
2 + 16
2 = c
2
a+c = 32 => a = 32− c , gdzie c <32 i c>0
podstawiając do drugiego równania mamy:
( 32 −c)
2 + 256= c
2
1024 −64c + c
2 +256 = c
2 => 64c= 1280 =>
c = 20
to a= 32 − 20 =>
a= 12
boki trójkata są :
a= 12 b= 16 c= 20
teraz
Muszę narysować Ci rysunek , bo Twój nie ma oznaczeń
Jesteś jeszcze?... czy już śpisz?
Eta:
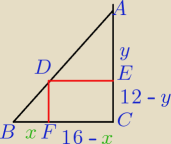
ΔBFD ~ Δ DEA
to:
po przekształceniu:
4x +3y= 48 => x = 16 −
43y
P= ( 16 −x)( 12−y)
więc:
P( y) = ( 16 − 16 +
43y)( 12 −y)
P(y)= −
43y
2 + 16y
y
max = 6 więc x
max = 16 −
43*6
x
max = 8
zatem prostokąt ma wymiary: 6 i 8
Miłych snów
z kawalka tektury w ksztalcie trojkata prostokatnego o obwodzie 48 ktorego dlugosc bokow tworzy
ciag arytmetyczny nalezy wyciac prostokat o najwiekszym polu powierzchni wyznacz jego wymiary
!