zadania zadanie: wyznacz zbior wszystkich srodkow cieciw paraboli o rownaniu y=x2 przechodzacych przez punkt A(0,2)

zadanie: ?

MQ: Pęk prostych: y−2=ax podstawiasz do r. paraboli: ax+2=x² Δ wychodzi a²+8, więc zawsze >0 stąd warunek na a: a∊R Liczysz x₁ i x₂ a potem średnią z nich −−− dostajesz wsp. x−ową środka cięciwy albo bezpośrednio ze wzoru Viete'a w każdym razie powinno ci wyjść x_s=a podstawiasz a do równania prostej i dostajesz równanie na y_s powinno ci wyjść: y_s=a²+2, czyli w końcu: y_s=x_s²+2 czyli zbiór punktów to parabola y=x²+2

zadanie: w odp. jest y=2x²+2

zadanie: jak wyglada do tego rysunek? te cieciwy?

zadanie: ?

MQ: Fakt, pomyłka, ale... wg mnie: x_s=a/2 y_s=a²/2+2

zadanie: a rysunek jakby wygladal z tymi cieciwami?

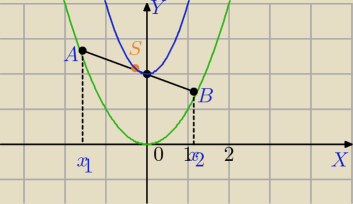
Mila: y=x² y=ax+2 Równanie prostej przechodzącej przez (0;2) i przecinającej parabolę w dwóch punktach. A=(x₁;ax₁+2) B=(x₂;ax₂+2)

	x1+x2		ax1+2+ax2+2		x1+x2		a(x1+x2)+4
S=(		;		=(		;		)=
	2		2		2		2

	x1+x2		a(x1+x2)
S=(		;		+2)
	2		2

A i B punkty przecięcia paraboli i prostej x²=ax+2⇔ x²−ax−2=0 Δ=a²+8>0 równanie ma 2 rozwiązania dla a∊R x₁+x₂=a w takim razie

	a		a*a		a		a2
S=(		;		+2)=(		;		+2})
	2		2		2		2

	a		a2		4x2
przyjmując x=		⇒a=2x to y=		+2=		+2
	2		2		2

y=2x²+2 wykres niebieski.

Mila: ?