geometria analityczna , proszę o pomoc matem: Witam ma wielki problem z rozwiązaniem dwóch zadań z geometrii analitycznej dopiero zaczynam ten dział realizować więc prosiłbym o omówienie krok po kroku jak zrobić te zadania bo w ogóle sobie z nimi nie radze : zad 1 Znajdź równanie prostej k przechodzącej przez punkt P(2,5) , która ogranicza wraz z dodatnimi pół osiami układu współrzędnych trójkąt o polu równym 36. zad 2 w prostokącie ABCD dane są : wierzchołek C(−2,2) i wektor AB =[3,3]. Wyznacz równania prostych , zawierających przekątne tego prostokąta , jeśli wiadomo że wierzchołek A należy do prostej o równaniu x−2y=0

Artur_z_miasta_Neptuna: 1) krok 1 ... rusynek układu współrzędnych i zaznaczymy punkt P krok 2 ... zauważamy, że trójkąt będzie trójkątem prostokątnym ... a prosta będzie przechodziła przez punkty: S=(x₁,0) oraz W=(0,y₂)

	x1*y2
krok 3 ... w takim razie		= PΔ = 36
	2

krok 4 ... ogólny wzór prostej: y=ax+b krok 5 ... podstawiasz punkt S, W i P: 0 = a*x₁ + b y₂ = 0 + b 5 = a*2 + b oraz:

x1*y2
	= 36 <−−− ograniczenie pola
2

masz układ czterech równań z czteroma niewiadomymi ... rozwiąż

matem: aha to to pierwsze zadanie już rozumiem to sobie juz rozwiąże a mógłbyś mi też tak jasno wytłumaczyć zadanie drugie w tych krokach najlepiej bo wtedy wiem co należy najpierw zrobić

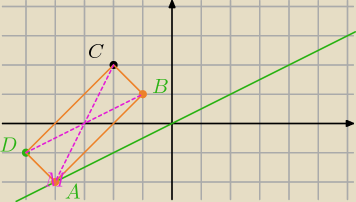
Mila: 2) AB =[3,3] DC^→=AB^→(boki przeciwległe równe i równoległe) C=(−2;2)→T[−3;−3]→D=(−2+(−3);2−3)=(−5;−1)

	1
x−2y=0⇔2y=x⇔y=		x
	2

	1
A=(x;		x) i DA→⊥AB→
	2

	1
wektor DA → =[x+5;		x+1]
	2

Iloczyn skalarny wektorów prostopadłych jest równy 0.

	1
3*(x+5)+3*(		x+1)=0
	2

x=−4

	1
y=		*(−4)=−2
	2

A=(−4;−2) punkt B otrzymasz przesuwając A o wektor AB=[3,3] A=(−4;−2)→T[3;3]=B=(−1;1) mając wierzchołki możesz pisać równania prostych AC i DB Czy umiesz pisać równania prostych?

matem: no jeszcze nie umiem pisać tych równań prostych jak sie ma dwa punkty ale właśnie chciałem się spytać czy nie można sprawdzić podstawiając pod równanie kierunkowe y=ax+b czy musi być to ogólne Ax +By+C=0 ? I czy w ogóle jest jakaś różnica czy korzystam z równania na ogólną prostą czy z równania kierunkowego? Bo z tego co wiem to tam jakiś wzorek był na prostą przez którą przechodzą dwa punkty no i właśnie nie wiem czym to sie różni czy podstawie do ogólnej czy do kierunkowej postaci prostej

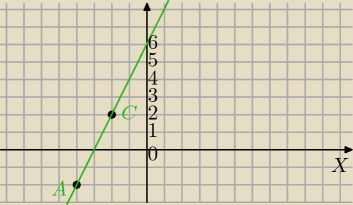
Mila: Wybierasz dowolną postać.( to co lepiej Ci się liczy) Ja myślę, że łatwiej Ci będzie r. kierunkowe. Ja robię tak: prosta AC: A=(−4;−2); C=(−2;2) y=ax+b podstawiam wsp.punktów −2=−4a+b 2=−2a+b odejmuję stronami −4=−2a⇔a=2 podstawiam 2=−2*2+b⇔b=6 (patrzę czy prosta AC przecina oś y w p.6 , to taka samokontrola,) AC: y=2x+6

matem: aha wielkie dzięki

matem: a jest jakiś inny sposób zrobienia zadania 1?

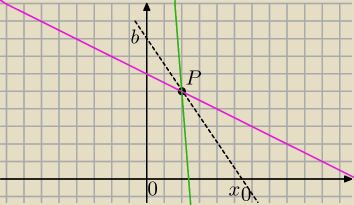
Mila: Szkic y=ax+b 5=2a+b⇔b=5−2a a<0 i b>0 y=ax+5−2a x₀ − miejsce zerowe funkcji y=ax+5−2a ax+5−2a=0 ax=2a−5

	2a−5
x0=
	a

	1
P=		|x0|*|b|=36
	2

	2a−5
|		|*|5−2a|=72
	a

zał.a<0 ⇔5−2a≥0 równanie możemy zapisać

2a−5
	*(5−2a)=72
a

(2a−5)(5−2a)=72a rozwiąż

	1
a=−		lub a=−12,5⇔
	2

	1
b=5−2a=5−2*(−		)=6 lub b=5−2*(−12,5)=30
	2

proste

	1
y=−		x+6 lub y=−12,5x+30
	2

sprawdź czy pole równe 36.