.. Edu: Mam problem z liczeniem największej i najmniejszej wartości funkcji w przedziałach, czy mógłby mi ktoś to troche objaśnić?

Aga1.: Podaj przykład, czy masz na myśli funkcję kwadratową, czy trzeba zastosować pochodne?

Edu: zadanie z pochodnych:

	1		5
a)		x3 −		x2 + 4x x∊<0,3>
	3		2

	3
b)x5−5x x∊(−2,		)
	2

Edu:

	3
w b przedziały zamknięte x∊<−2,		>
	2

Aga1.:

	1		5
f(x)=		x3−		x2+4x
	3		2

1. Oblicz pochodną tej funkcji.

Aga1.:

Edu: pochdna a) x² − 5x + 4 pochodna b) 5x⁴ − 5

Aga1.: Ok. Teraz pochodną przyrównaj do 0 i oblicz miejsca zerowe pochodnej. Czyli rozwiąż równanie a)x²−5x+4=0 i b podobnie.

Edu: a) x₁ = 1 x₂ = 4 i ja bym policzył f(0) i f(p) p=2,5 ale w odpowiedzi jest ze f(0)i f(3) patrzac największą i najmniejszą wartość to patrze na wykresie f(x) − wielomianu czy f'(x) − f.kwadratowej ?

Mila: Witaj Aga.

Edu:

Aga1.: Nie, funkcja f może przyjąć najmniejszą lub największą wartość tylko w punktach, gdzie pochodna równa się 0 lub na krańcach przedziału. liczysz (podstawiasz do podanego wzoru) f(0)= f(3)= i f(1)= Nie liczysz f(4), bo 4∉<0,3>

Aga1.: Witaj Mila.

Edu: ahaa, czyli msuze policzy wszystkie podane punkty w przedziale i wtedy zobaczyc który jest maksimum i minimum tak? a co z tym p ?

Aga1.: Tak,p liczysz przy funkcji kwadratowej i wówczas nie bawisz się w pochodną.

Edu: jak bede miał np f(x) = x² + 3 − 2 nie musze liczyc pochodnej?

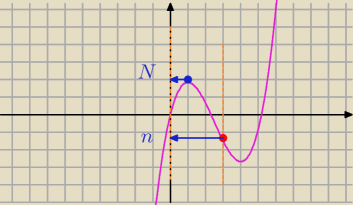
Mila: Edu, popatrz na wykres Agi , to jest wykres f(x).

	5
największa wartość dla x=1 (f(1)=1		) maksimum lokalne ( pochodna równa 0)
	6

najmniejsza − liczysz na końcach przedziału f(0)=0 f(3)=−1,5 (sprawdź rachunek)

Edu: ok, proszę pomóż mi jeszcze w b, tam robię tak f'(x" = 5x⁴ − 5 = 5(x⁴ − 1) x=1 x=1 x= −1 x= −1 dobrze wyliczam pierwiastki?

Aga1.: x⁴−1=0 (x²−1)(x²+1)=0 x²−1=0 v x²+1=0 ( nie ma rozwiązań. x=1 v x=−1

Edu: nie ma rozwiązań dlatego ze x² nie może być ujemny tak?

Edu: tak?

Artur_z_miasta_Neptuna: tak

Edu: ok dzięki