Zadanie dla chętnych - stereometria
qwerty: Zadanie dla chętnych − stereometria
Dzisiaj znalazłem w książce zadanie dla chętnych ze stereometrii:
Dany jest ostrosłup o podstawie rombu, o boku długości a oraz kącie ostrym γ. Wiemy, że jedna
ze ścian bocznych jest prostopadła do płaszczyzny podstawy. Płaszczyzny przechodzące przez
wierzchołek ostrosłupa i przekątne podstawy tworzą z płaszczyzną podstawy kąty α i β. Obliczyć
objętość danego ostrosłupa.
15 sty 21:36
qwerty: Odświeżam.
15 sty 22:52
Skipper:
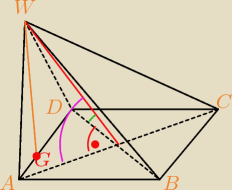
... wydaje się proste ... tylko liczenia "od regimenta i ciut"
Znając długości przekątnych podstawy oraz kąty α i β policzymy |AW| i |DW|
Potem rozwiązując trójkąt ADW policzymy wysokość |WG|
15 sty 23:31
qwerty: W jaki sposób mamy policzyć bok |AW| ?
16 sty 07:28
Nienor: Mając γ i a obliczysz długość przekątnych. Mając połowę płaszczyzny j kąt α obliczyć powinieneś
|AW|. Jeśli dobrze zrozumiałam zadanie i rysunek.
16 sty 09:12
qwerty: Ale przecież nie mamy danego kąta CAW, ani tego drugiego, w tym trójkącie mamy daną tylko
połowę przekątnej i kąt α, z tego drugiego boku nie policzymy.
16 sty 12:44
qwerty: Odświeżam.
16 sty 16:28
qwerty: Odświeżam.
16 sty 18:37
qwerty: Odświeżam.
17 sty 17:45
Mila: 1) napisałeś, że dla chętnych, zamiast, że potrzebna Ci pomoc.
2) czy masz odpowiedź?
17 sty 17:47
qwerty: Zadanie dla chętnych, do którego potrzebuje pomocy

| | a3 * sinγ * sinγ2 * tgα*tgβ | |
V = |
| |
| | 3(tgγ2*tgβ+tgα) | |
17 sty 18:07
Artur_z_miasta_Neptuna:
a z czym konkretnie nie możesz sobie poradzić

17 sty 18:10
qwerty: Z tym, że wg mnie rozwiązanie (sposób rozwiązania podany przez Skippera) jest niepoprawne,
oznaczmy sobie ten punkt przecięcia AC i BD przez jakieś E. W trójkącie AWE mamy dany bok |AE|
oraz kąt <WEA = α, stąd nie wyliczymy długości boku |AW|, być może Skipper przyjął błędne
założenie, że <WAE = 90*
17 sty 18:41
Mila:
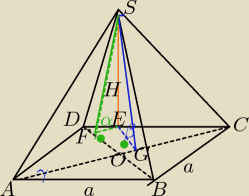
Sciana DSC jest prostopadła do płaszczyzny podstawy
Wg tego rysunku, wynik zgadza się.
Oblicz OD i OC
H=|FE| *tgα
H=|GE|*tgβ
|FE| *tgα=|GE|*tgβ
|OG|=|FE|
ΔCEG∼ΔCDO
dalej poradzisz sobie.
18 sty 16:21
 ... wydaje się proste ... tylko liczenia "od regimenta i ciut"
Znając długości przekątnych podstawy oraz kąty α i β policzymy |AW| i |DW|
Potem rozwiązując trójkąt ADW policzymy wysokość |WG|
... wydaje się proste ... tylko liczenia "od regimenta i ciut"
Znając długości przekątnych podstawy oraz kąty α i β policzymy |AW| i |DW|
Potem rozwiązując trójkąt ADW policzymy wysokość |WG|


 Sciana DSC jest prostopadła do płaszczyzny podstawy
Wg tego rysunku, wynik zgadza się.
Oblicz OD i OC
H=|FE| *tgα
H=|GE|*tgβ
|FE| *tgα=|GE|*tgβ
|OG|=|FE|
ΔCEG∼ΔCDO
dalej poradzisz sobie.
Sciana DSC jest prostopadła do płaszczyzny podstawy
Wg tego rysunku, wynik zgadza się.
Oblicz OD i OC
H=|FE| *tgα
H=|GE|*tgβ
|FE| *tgα=|GE|*tgβ
|OG|=|FE|
ΔCEG∼ΔCDO
dalej poradzisz sobie.