Bogdan:
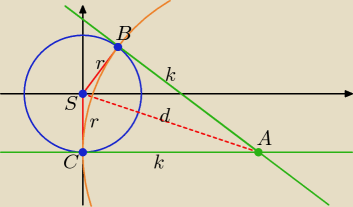
Okrąg: x
2 + y
2 = 4, S = (0, 0), r = 2.
d = |CS| =
√36 + 4 =
√40 = 2
√10
k = |SB| = |SC| =
√d2 − r2 =
√40 − 4 = 6.
Tworzymy okrąg o środku A = (6, −2) i promieniu k = 6: (x − 6)
2 + (y + 2)
2 = 36.
Rozwiązujemy układ dwóch równań:
1. x
2 + y
2 = 4
2. (x − 6)
2 + (y + 2)
2 = 36
Rozwiązaniem tego układu są liczy będące współrzędnymi punktów styczności: B, C.
Teraz piszemy równanie prostej przechodzącej przez punkty A, B oraz równanie prostej
przechodzącej przez punkty A, C. Są to równania szukanych stycznych.