Argument główny liczby zespolonej John : Witam, mógłby ktoś mi wytłumaczyć jak wyznacza się argument główny liczby zespolonej np. na tym przykładzie? z=−2+2i

John : Pomoże ktoś?

MQ: z=a+bi=r(cosφ+i*sinφ) arg(z)=φ wzięte z przedziału <0,2π)

Aga1.: r=√a²+b²=√(−2)²+2²=2√2

	−2		√2
cosφ=		=−
	2√2		2

	√2
sinφ=
	2

φ=

John : Wlasnie o co chodzi z tym przedzialem? Jak mi wyjdzie liczba ktora przekracza ten przedzial to co wtedy robie? Bo sam sposob liczenia argumentu rozumiem.

MQ: O to chodzi, że szukasz rozwiązania dla φ z tego przedziału. Funkcje cos i sin są okresowe i do rozwiązania można wybrać dowolny przedział o długości 2π. Ty masz wybrać przedział <0,2π).

John : Ok dzięki.

John : A jeszcze jedno pytanie: jak rozumiec arg(modul z)?

MQ: moduł z jest liczbą rzeczywistą dodatnią (chyba że 0) więc jego argument będzie równy 0. Dla modułu =0 argument jest nieokreślony.

John : Nie rozumiem. To jak rozwiązac 0<arg(modul z)≤2π/3 ?

John : Dobra mam to będzie odbicie tego kąta względem osi rzeczywistej.

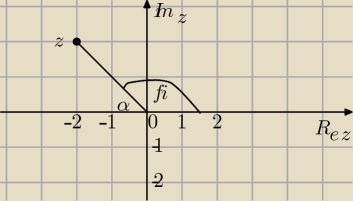
Mila: Liczba z=−2+2i to punkt (−2;2) na płaszczyźnie Z ilustracji widzisz, że to kąt II ćwiartki

	π
α=
	4

	π
φ=π−
	4