trójkąt Zuzia: Na kole o promieniu 4 cm opisano trójkąt prostokątny. Wyznacz długość boków tego trójkąta, który ma najmniejsze pole. można użyć pochodnych

Zuzia:

Zuzia: pomoże ktoś?

Zuzia: pomocy

Zuzia: ?

Skipper:

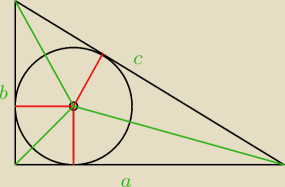
	ar		br		cr		r
pole trójkąta to		+		+		=		(a+b+c)
	2		2		2		2

zatem najmniejsze pole ma trójkąt o najmniejszym obwodzie ...itd

Zuzia: oj to pochodnymi się robi tak to mogę sobie sama pomyślec

Zuzia: to coś bardziej że p= (b*a)/2 b=x+4 c=y+x a=4+y ♦ a²+b²=c² i wliczamy x z tego ♦ równania i wstawiamy w ten wzór od pola poźniej liczymy pochodną p'(x) pomoże ktoś?

Mila: wg oznaczeń Zuzi: (x+y)²=(x+4)²+(y+4)²

	4x+16
y=
	x−4

	x2+4x
P=4*(		(lepiej liczyć wg wzoru Skippera)
	x−4

Licz pochodną, masz odpowiedź do zadania?

Skipper: 16+8y+y²+16+8x+x²−x²−2xy−y²=0 8y−2xy+8x+32=0 −2y(x−4)+8(x+4)=0

	4(x+4)
y=
	x−4

	2x(x+4)		2x2+8x
P=		=
	x−4		x−4

szukamy P_min

	(4x+8)(x−4)−2x2−8x
P'=
	(x−4)2

war.konieczny P'=0 itd