pomocy !!!!!!!!!!!!!!!!!!! na jutro pilne!!!
karolinkowata: pomocy ludzie...Krawędź podstawy graniastosłupa prawidłowego sześciokątnego ma długość a. Jaką
wysokość powinien mieć ten graniastosłup aby trójkąt zbudowany z przekątnej ściany bocznej
dłuższej przekątnej podstawy i krótszej przekątnej graniastosłupa był
równoramienny?(potrzebuje do tego zadania rysunek plus opis całego zadania co i jak po koleji
jest zrobione ) prosze
!
dero2005:
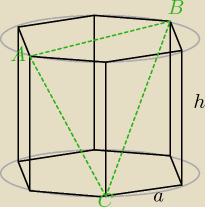
AB = 2a ⇒ przekątna większa podstawy
AC =
√a2 + h2 ⇒ przekątna ściany bocznej
CB =
√(a√3)2 + h2 ⇒ przekątna mniejsza graniastosłupa
sprawdzamy pierwszą możliwość
AC = CB
√a2 + h2 =
√(a√3)2 + h2 |
2
a
2 + h
2 = 3a
2 + h
2
0 = 2a
2 ⇒ równanie sprzeczne
sprawdzamy dalej drugą możliwość
AB = AC
2a =
√a2 + h2 |
2
4a
2 = a
2 + h
2
3a
2 = h
2
h = a
√3
Trzecia możliwość
AB = BC
2a =
√(a√3)2 + h2 |
2
4a
2 = 3a
2 + h
2
h
2 = a
2
h = a
Podsumowanie
jeśli h = a to ramiona trójkąta będą stanowiły większa przekątna podstawy i krótsza przekątna
graniastosłupa, jeśli h = a
√3 to ramiona trójkąta bedą stanowiły dłuższa przekątna podstawy
i przekątna ściany bocznej
