Miś Uszaty:
Równośc
1
*) tg(α+l)=tgα zachodzi przy dowolnej dopuszczalnej wartości α i przy l=π
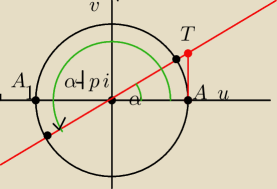
Widzimy że końce łuków α i α+π są diametralnie przeciwległe i i mają tę samą linię tangensa
AT
wobec tego
tg(α+π)=tgα
Należałoby jeszcze wykazać ze l=π jest najmniejszą liczba dodatnia spełniająca równość 1
*)
przy dowolnym dopuszczalnym x
Podstawiając w równości 1
*) x=0 otrzymujemy
tgl=0
Wtedy odcinek AT degeneruje się do punktu i punkt T pokrywa się z punktem A
Dla końca łuku(l) możliwe są dwa położenia A=(1,0) i A
1=(−1,0)
Najmniejsza dodatnia wartość łuku (l) przy której AT=0 jest l=π
 α
α
 Równośc
1*) tg(α+l)=tgα zachodzi przy dowolnej dopuszczalnej wartości α i przy l=π
Widzimy że końce łuków α i α+π są diametralnie przeciwległe i i mają tę samą linię tangensa
AT
wobec tego
tg(α+π)=tgα
Należałoby jeszcze wykazać ze l=π jest najmniejszą liczba dodatnia spełniająca równość 1*)
przy dowolnym dopuszczalnym x
Podstawiając w równości 1*) x=0 otrzymujemy
tgl=0
Wtedy odcinek AT degeneruje się do punktu i punkt T pokrywa się z punktem A
Dla końca łuku(l) możliwe są dwa położenia A=(1,0) i A1=(−1,0)
Najmniejsza dodatnia wartość łuku (l) przy której AT=0 jest l=π
Równośc
1*) tg(α+l)=tgα zachodzi przy dowolnej dopuszczalnej wartości α i przy l=π
Widzimy że końce łuków α i α+π są diametralnie przeciwległe i i mają tę samą linię tangensa
AT
wobec tego
tg(α+π)=tgα
Należałoby jeszcze wykazać ze l=π jest najmniejszą liczba dodatnia spełniająca równość 1*)
przy dowolnym dopuszczalnym x
Podstawiając w równości 1*) x=0 otrzymujemy
tgl=0
Wtedy odcinek AT degeneruje się do punktu i punkt T pokrywa się z punktem A
Dla końca łuku(l) możliwe są dwa położenia A=(1,0) i A1=(−1,0)
Najmniejsza dodatnia wartość łuku (l) przy której AT=0 jest l=π