Funkcje Robal: Dana jest funkcja f określona wzorem {x² dla xE (−2,2> {x−6 dla x(−nieskonczonosc,−2> {−2x+6 dla x(2,+nieskończoność). Liczba miejsc zerowych to? Nie chce odpowiedzi, chce wiedzieć jak to obliczyć, łopatologicznie.

ja: f(x)=0 i sprawdzasz przedziałami czyli np 1. x∊ (−2,2> f(x)=0 0=x² i sprawdzasz czy wynik należy do twojego przedziału czyli w tym przypadku (−2,2> itd

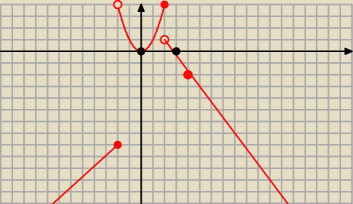
Mila: 1)x²=0⇔x=0 i 0∊(−2,2> ⇔x=0 jest miejscem zerowym 2) x−6=0⇔x=6 i 6 ∉(−∞; −2) no to nie jest miejscem zerowym 3) −2x+6=0 −2x=−6 x=3 liczba 3 ∊(2;∞) w takim razie jest miejscem zerowym odp 2 miejsca zerowe II sposób graficznie

ZK: Powiadasz kolego ze chcesz lopatologicznie . Tylko czemu tak pozno. Musisz kazda z tych funkcji z osobna przyrownac do 0 i zbaczyxc czy rozwiazanie nalezy do przedzialu. Powiem CI kolego ze ciekawie bedzie przy x²=0 ⇒x=0 wiec 0∊(−2,2> Moze niech sie wypowiedza inni czy to 0 potraktowac jako jedno miejsce zerowe czy jako podwojne miejsce zerowe . Teraz x−6=0 to x=6 czy 6 nalezy do przedzialu (−∞,−2> . Nie −wiec ta funkcja okreslona tym wzorem dla tego przedzialu nie ma miejsca zerowego Teraz −2x+6=0 to −2x=−6 to x=3 teraz czy 3 nalezy do (2,∞) . Oczywiscie ze tak ., Wiec funkcja okreslona tym wzorem dla x∊(2,∞) ma jedna miejsce zerowe x=3 Masz to lopatologicznie . Nie masz odpowiedzi bo musisz zdecydowac co do ilosci miejsc zerowych dla x²=0 i x(−2,2>

Mila: Miejsce zerowe− argument dla którego funkcja przyjmuje wartość równą zero.

Aga1.: Funkcja y=x² ma jedno miejsce zerowe dla x ∊(−2,2>

ZK: Przeczytalem teraz tez post PW z innego zadania gdzie wyjasnil dlaczego jedno miejsce zerowe .