Stereometria Adam: Potrafi ktoś zrobić to zadanie? Oblicz cosinus kąta zawartego między ścianami bocznymi: −czworościanu foremnego, −ostrosłupa prawidłowego czworokątnego, którego ściany boczne są trójkatami równoramiennymi o ramieniu dwa razy dłuższym od krawędzi podstawy.

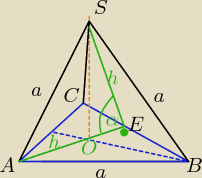
Mila: Wszystkie ściany są Δ równobocznymi o boku a z tw. cosinusów w ΔAES: a²=h²+h²−2h*h cosα

	a√3
h=		wysokość Δrównobocznego o boku dł.a
	2

	3a2		3a2		3a2
a2=		+		−2*		cosα
	4		4		4

	1		3
−		a2=−		cosα
	2		2

	1
cosα=
	3

II sposób w ΔSOE:

	1   h 3		1
cosα=		=
	h		3

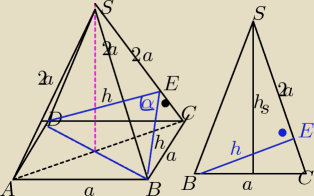
Mila: 2)Ztw. cosinusów w ΔBDE: |DB|²=h²+h²−2h*h*cosα Musisz obliczyć h z porównania pola ΔBCS

1		1		1
	a*hs=		*2a*h⇔h=		hs
2		2		2

	1		15a2
hs2=(2a)2−(		a)2=
	2		4

	a√15
hs=
	2

spróbujesz sam dokończyć?

Aragon: Wyszło mi, że IDB|=2a², wiadomo h= a* √15/4, więc z tw. cosinusów wychodzi, że cosα=9/15? Chyba coś pomieszałem, bo powinno być −1/15.

Mila: h=U{a√15{4}

	a2*15		a2*15		a2*15
2a2=		+		−2*		cosα
	16		16		16

	30a2		a2*15
2a2=		−		cosα /:a2
	16		8

	15		15
2−		=−		cosα
	8		8

1		15
	=−		cosα
8		8

	1		−8		−1
cosα=		*		=
	8		15		15

Aragon: A rozumiem już, dziękuję. W tw. cosinusów a2=h2+h2−2h*h cosα, myślałem, że jest 2*h*h, a tam się omija jakby to jedno h, więc coś innego powychodziło.