W trójkącie prostokątnym na dłuższej przyprostokątnej jako na średnicy opisano o dfghjk: W trójkącie prostokątnym na dłuższej przyprostokątnej jako na średnicy opisano okrąg. Wyznacz długość okręgu, jeżeli krótsza przyprostokątna jest równa 30, a cięciwa łącząca wierzcho− łek kąta prostego z punktem przecięcia przeciwprostokątnej z okręgiem (różnym od wierzchoł− ków trójkąta) jest równa 24.

Eta: Ob okręgu = 40π

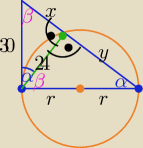
Eta: Rysunek powinien wszystko rozjaśnić Dokończ ........

dfghjk: ale jak byś mógł opisać jak do tego doszedłeś

dfghjk: i ten obrazek jest chyba źle. Bo masz 1 trójkąt gzie przy kącie alfa bok ma 24 i 2 trójkąt gdzie przy kącie beta bok ma 24

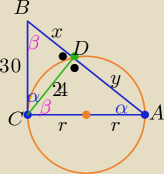
Eta: |∡CDA|= 90^o , bo jest to kąt wpisany oparty na średnicy zatem trójkąty CDA i CDB są prostokątne i są podobne z cechy (kkk) Zastosuj tw. Pitagorasa i .... otrzymasz x= 18 i y= 32 i 2r= 40

dfghjk: aaaa dzieki

dfghjk: a jak obliczyłeś y

Eta: z podobieństwa trójkątów CDA i CDB:

	|CD|		y
		=		⇒ |CD|2= x*y ⇒ y=........
	x		|CD|