Rozwiąż nierówność wielomianową Łukasz : Witam mam straszny problem z rozwiązaniem tej nierówności będę bardzo wdzięczny za pomoc. (x−4)(x⁵−3x⁴−4x³+8x²−24x−32)>0

PW: 24=8^.3 i 32=8^.4, to podpowiada jak grupować.

Łukasz: x⁵−3x⁴−4x³+8x²−8x*3−8*4 i dalej nie wiem co z tym zrobić /

Łukasz: Podzieliłem ten wielomian przez 2 i wyszło mi x⁴−x³−6x²+4x²−16

Aga1.: Ale dwa nie jest pierwiastkiem , podziel przez x−1.

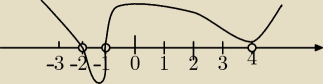
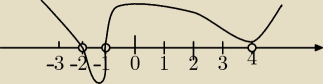Mila: w(1)=1−3−4+8−24−32≠0 w(−1)=−1−3+4+8+24−32=0 x⁵−3x⁴−4x³+8x²−24x−32):(x+1)=x⁴−4x³+8x−32 Horner 1 −3 −4 8 −24 −32 x=−1 1 −4 0 8 −32 0 Q(x)=x⁴−4x³+8x−32=(x³(x−4)+8(x−4)=(x−4)*(x³+8)=(x−4)(x+2)(x²+2x+4) (x⁵−3x⁴−4x³+8x²−24x−32)=(x+1)*(x−4)*(x+2)(x²+2x+4) Wracamy do nierówności (x−4)(x+1)*(x−4)*(x+2)(x²+2x+4)>0⇔ (x+1)*(x−4)²*(x+2)(x²+2x+4)>0 [(x²+2x+4)>0 każdego x∊R) ⇔(x+1)*(x−4)²*(x+2)>0 Miejsca zerowe: x=−1,x=−2,x=4 podwójny x∊(−∞;−2)∪(−1;4)∪(4;∞)