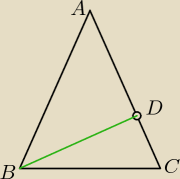
srodkowa w trojkacie rownoramiennym stasia: Witajcie, probuje rozwiazac pewne przykladowe zadania konkursowe i mam w jednym problem. Zadanie brzmi: Podstawą trójkąta równoramiennego ABC jest bok BC. Na boku AC leży taki punkt D, że odcinki DA i DB są równe oraz kąty DBA i DBC są równe. Oblicz miarę kąta BAC. Nie mam pojecia jak wyznaczyc te katy,bo tak naprawde jest dla mnie za malo danych. Gdybym przyjela ze srodkowa poprowadzona z wierzcholka B do boku AC jest jego wysokoscia, to kat przy podstawie wyszedlby mi jak w trojkacie rownobocznym i w ogole mialabym do czynienia z trojkatem rownobocznym/ Nie zakladajac nic, ja moge brac dowolne miary katow tak aby te warunki z zadania sie zgadzaly,np. katy przy podstawie maja po 20 stopni ,a ten szukany 140. Jak sobie poradzic z tym zadaniem? Prosze o pomoc.

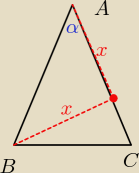
Artur_z_miasta_Neptuna: skoro |AD| = |BD| to Δ_ABD jest równoramienny czyli ∡BAD = ∡DBA w zadaniu masz podane, że ∡DBA = ∡DBC ... czyli ∡CBA = 2*∡DBA a wiesz że Δ_ABC jest równoramienny więc ∡CBA = ∡BCA = 2*∡DBA = 2*∡BAD = 2*α stąd 5α = 180 ⇒ α = ...

Skipper: 36

stasia: faktycznie,dzieki