Własności kątów Kamil: Dany jest kąt ostry α i punkt P leżący wewnątrz kąta na jego dwusiecznej i w odległości d od wierzchołka kąta. Wówczas najmniejszy obwód trójkąta o jednym wierzchołku w punkcie P a pozostałych wierzchołkach po jednym na każdym z ramion kąta wynosi: a) 2d*tg(α/2) b) d*tg(α/2)[1 + 2cosα] c) 2d*tg(α/2)[1 + cosα] d) d*tg(α/2)[1 + cosα]

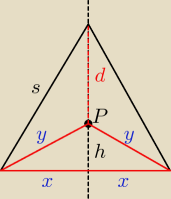
Artur_z_miasta_Neptuna: Obw = 2x+2y

x
	= tg(α/2)
d+h

y = √x²+h² y² = d²+s² − 2d*s*cos(α/2) s = √x²+(d+h)² układ czterech równań z czterema niewiadomymi −−− powodzenia