stożek domczis: przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 6. Wysokość tego trójkąta opuszczona na ramię jest równa 4√2. Oblicz objętość i pole powierzchni bocznej tego stożka

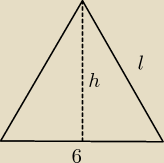
Gall: Długość podstawy trójkąta o długości 6 jest średnicą podstawy stożka czyli 2r. Wysokość stożka h=4√2. Obliczenia: −objętość stożka V V=1/3 *π*r²*h V= 1/3*π*3²*4√2 = 12π√2 −powierzchnia boczna stożka tworząca stożka l obliczmy z tw.Pitagorasa l = √h²+r² = √32+9 = √41 Pb = πrl = 3√41π

Janek191: Miało być : wysokość trójkąta opuszczona na ramię , a nie na podstawę.

Janek191: Mamy r = 3 l*4√2 = 6 *h => l = ( 6 h)/( 4 √2 ) h² + 3² = l² −−−−−−−−−−−−−−−−−−−−−−− h² + 9 = (36 h²)/ 32 / * 32 32 h² + 288 = 36 h² 4 h² = 288 / : 4 h² = 72 = 36*2 h = 6 √2 =========== Objętość stożka V = (1/3) Pp*h = (1/3) π r² *h = (1/3) π *3² * 6 √2 = 18 p{2] π ======================================================= l² = h² + 9 = ( 6 √2)² + 9 = 72 + 9 = 81 l = 9 −−−−−−− Pole powierzchni Pc = π r² + π r*l = π *3² + π*3*9 = 9π + 27π = 36π ============================================= Pb = π r*l = π * 3* 9 = 27 π =========================