Witam! Prosba o sprawdzenie. aa: Proszę o sprawdzenie Witam! Mam takie polecenie aby zamienic postac parametryczna prostej na ogólna i robie to tak: { x= 2+3t { y=−1−2t, gdzie t ∊R wypisuję punkt A = (2,−1) oraz wektor u=[3,−2] a następnie robię tak: 3 = x₂ −2 x₂ = 5 −2 = y₂ +1 y₂ = −3 czyli pkt. B=(5,−3) a nastepnie robie uklad rownan i obliczam postac kierunkowa prostej, co w tym wypadku wychodzi mi y = −2/3x + 1/3. Prosze o sprawdzenie poprawnosci tej metody, gdyz tak naprawde sam ją wymyslilem i raczej tak na czuja Jezeli bylaby mozliwosc, moze da sie to jakos skrocic? Pozdrawiam!

PW: Sam wymyśliłeś, i to jest najcenniejsze. Szybka metoda to wyliczenie t z obu równań i przyrównanie. Dla każdej t

	x−2		−y−1
t=		i jednocześnie t=		, a więc
	3		2

	x−2		−y−1
		=		,
	3		2

a to już będzie postać ogólna po prostych przekształceniach (sprawdź, że ten sam wynik, tyle że Ty napisałeś postać kierunkową).

aa: jasne, dziękuje bardzo Bede korzystał z Twojej metody jak i z mojej Dziękuje za precyzyjną odpowiedz, taką jakiej oczekiwałem Pozdrawiam!

aa: To zadam jeszcze jedno pytanko. Jak mam na podstawie postaci parametrycznej prostej wyznaczyc do niej prosta równoległa//prostopadłą. To muszę tę pierwszą zamieniac na kierunkową , wyznaczyć drugą i wtedy zamienic tę drugą na postac parametryczna czy jest tez jakis łatwiejszy sposób?

aa: to jak? : )

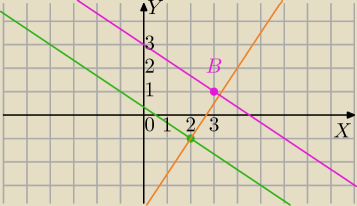
Mila: Dana prosta, równanie parametryczne: x= 2+3t y=−1−2t równanie kierunkowe:

	2		1
m: y=−		x+		(zielony wykres)
	3		3

Prostopadła przechodząca przez A(2;−1) w postaci parametrycznej: x=2+2t y=−1+3t Postać kierunkowa:

	x−2
x−2=2t⇔t=
	2

	y+1		x−2		y+1		3
y+1=3t⇔t=		stąd		=		⇔y=		x−4 (pomarańczowa)
	3		2		3		2

Prosta równoległa do prostej m i przechodząca przez punkt B=(3,1) x= 3+3t y=1−2t postać parametryczna postać kierunkowa

	2		2
y=−		x+b i 1=−		*3+b⇔b=3
	3		3

	2
y=−		x+3
	3

pigor: ... weźmy "twój" przykład danej prostej (zamień miejscami współczynniki przy t i zmień znak jednego z nich na przeciwny) − patrz np. tak : k: (x,y)= (2+3t,−1−2t) ⇒ l: (x,y)= (2+2t, −1+3t) − szukana prosta l przechodząca przez dany punkt (2,−1) i ⊥ k, bo ich wektory kierunkowe są [3,−2] ⊥ [2,3], co wynika z zerowania się ich iloczynu skalarnego 3*2+(−2)*3= 6−6=0 tzn. cosinus kąta α miedzy nimi 0, a więc kąt α=90^o . ..

aa: Mila, z tego co napisałaś można wywnioskowac, że jak chce stworzyc z postaci parametrycznej dowolna prosta do niej rownolegla rowniez w postaci parametrycznej to wartosci przy t muszą być takie same, a jezeli prostopadłą to wartosci przy t muszę byc odwrotnie zapisane ( względem dołu i góry) czyz tak?

pigor: ... a na postaci kanonicznej widać to tak :

	x−2		y+1		x−2		y+1
k :		=		⇒ :		=		i l ⊥ k . ...
	3		−2		2		3

aa: aha, czyli w przypadku prostopadlosci zamieniami wartosci przy t gora z dołem a w przypadku rownoleglosci musza byc one takie same, tak? Czy mógłbym prosic o kilka przykładów? Co bym sobie mógł poćwiczyć? a i mam jeszcze 2 podpunkty takie dosyc trudne. a) wyznaczyc prostą rownoodległą od dwoch prostych b) wyznaczyc prosta będąca dwusieczne kąta wyznaczonego przez 2 proste. Jak sie robi takie rzeczy moze najpierw w postaci ogólnej lub kierunkowej a potem sam spróbuję coś wymyslec z postacią parametryczną

aa: Pigor a mógłbym np zamiast 3,−2 zmienic na 2,3 zmienic na −2,−3 ? Bo nie jest powiedziane ktorego znak mam zmienic

pigor: dla prostych l || k ich wektory kierunkowe te same , a zmienia się tylko punkt przez które przechodzi prosta l ....

aa: jasne, co do || rozumiem. a co do prostopadlych jak z tym znakiem? Moze byc rownie dobrze 2,3 jak i −2,−3?

pigor: jak najbardziej tak , co piszę wyraźnie powyżej "jednego z nich" . ...

aa: a czy mógłbyś mi podac kilka przykładów moze zebym sobie poćwiczył?

aa: albo wytłumaczył mi jak się przechodzi z postaci kierunkowej na postac parametryczna, to sobie samemu cos powymyslam. bo ja zawsze przechodzę tak, że piszę {x=t i y = ..... gdzie zamiast x wstawiam t A inaczej niestety nie umiem. A z tej postaci ciezko jest cos wyznaczyc prostopadlego badz rownoleglego..

pigor: mając postać kierunkową prostej wyznaczasz sobie jakieś w miarę ładne punkty tej prostej − np. przez dobieranie pary liczb (x,y) , a jak już je masz , to masz też wektor kierunkowy prostej i jeden z punktów, co wystarczy ci do postaci parametrycznej ... i tyle z mojej strony . ...

aa: a mógłbyś mi to rozpisac na jakims prostym przykładzie ?

Mila: 1) czy umiesz pisać równania prostych? 2) Jakie postacie równań prostych znasz? 3) jeśli masz równanie w postaci parametryczne to równoległa prosta ma ten sam wektor jak w przykładzie (1) u→=[3;−2] Prostopadła do danej prostej ma wektor v= [2;3] (odwrotnie wsp. i w jednej zmienić znak] u o v=3*2+(−2)*3 =0 iloczyn skalarny równy zero ( bo cos90⁰=0) Jeśli masz pytania, to jestem juz na forum

aa: chcialbym, abys jesli mogła, spróbowała mi rozpisac na przykładzie jak zamieniamy postac kierunkową na postac parametryczną. Reszte juz chyba umiem. Chodzi mi nie o zamianę , że x = t tylko o taką bardziej rozbudowaną jak w moim przykładzie. Ponieważ tego co napisał pigor tak za bardzo nie rozumiem.

Mila: Jeden ze sposobów. prosta y=2x+5 Wyznaczam 2 punkty należące do prostej x=0 to y=5 punkt A=(0;5) x=1 to y=7 punkt B=(1;7) AB^→=[1;2] równanie parametryczne: x=0+t y=5+2t lub x=1+t y=7+2t