skalowanie wykresow
Anita: Witam,
Mam pytanko. Jak wyskalować wykres sinusa dla y=f(πx) ? π>1 więc należy go "zciaśnić" o π razy.
czyli to oznacza, że teraz oś x bedzie przecięta w pkt π a nie π/2 ?
11 sty 11:33
Gustlik:
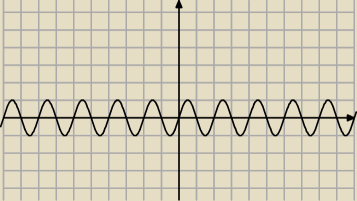
π
11 sty 11:35
Anita: bład w 2π a nie π ?
11 sty 11:35
Anita: a możesz mi wytłumaczyć dlaczego 1 kratka na x jest rowna jednej na y teraz ?
11 sty 11:36
Trivial:
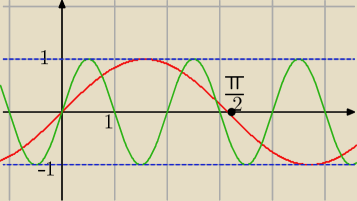
11 sty 11:46
Trivial:
| | π | |
Eh.... Na wykresie miało być π, a nie |
| |
| | 2 | |
11 sty 11:46
Anita: na wykresie jest mały błąd, zamiast π/2 powinno bycπ. i czy może ktoś mi to wytłumaczyć
| | x | |
dlaczego tak akurat to wygląda ? i dla przykładu f( |
| ) |
| | 2 | |
11 sty 11:48
Anita: to tak jakby było π/π tak ? gdyby było y=f(2x) to miałbym pierwsze przecięcie w pkt π/2 ?
11 sty 11:52
Trivial:
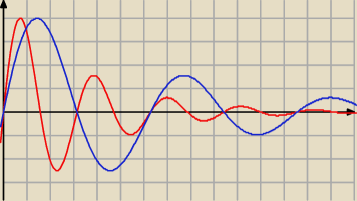
Rysując f(
ax) i patrząc z perspektywy osi x wszystko dzieje się
a razy szybciej niż
dla f(x).
| | x | | 1 | |
Czyli mając do narysowania np. f( |
| ) wszystko dzieje się |
| razy szybciej (czyli 2 |
| | 2 | | 2 | |
razy wolniej).
| | x | |
Czerwony to oryginalny wykres f(x), niebieski f( |
| ) |
| | 2 | |
11 sty 11:55
Trivial:
Wracając do wykresu sin(πx), skoro z perspektywy osi x wszystko dzieje π razy szybciej, to
mamy:
| | 1 | | π | |
dla x= |
| mamy to co mieliśmy dla x= |
| |
| | 2 | | 2 | |
dla x=1 mamy to co mieliśmy dla x=π
...
11 sty 12:01
Anita: Dzięki

11 sty 12:05
 π
π

 Rysując f(ax) i patrząc z perspektywy osi x wszystko dzieje się a razy szybciej niż
dla f(x).
Rysując f(ax) i patrząc z perspektywy osi x wszystko dzieje się a razy szybciej niż
dla f(x).
