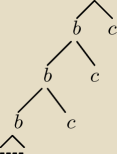
Probabilistyka sajm: Trzy zadania z prawdopodobieństwa: U_b*c−Urna z b kulami białymi oraz c czarnymi Losujemy bez zwracania jedną kule z urny U_4*1, oblicz prawdopodobieństwo wylosowania kuli czarnej w co najwyżej 3 losowaniu. Rysunek wyżej,

	4		1
w pierwszym wierszu prawdopodobieństwa b −		c −
	5		5

	3		1
w drugim wierszu prawdopodobieństwa b −		c −
	4		4

	2		1
w trzecim wierszu prawdopodobieństwa b −		c −		.
	3		3

	1		4		1		3		1		4		4		5		13
P(A)=		+		*		+		*		=		+		+		=
	5		5		4		4		3		20		20		20		20

sajm: Losujemy z urny U_1→3 trzy razy kule ze zwracaniem i wynik zapisujemy. Oblicz prawdopodobieństwo zdarzenia w którym suma wylosowanych kul wyniesie 6 a w jednym z dwóch pierwszych losowań wylosujemy kule z numerem 2. Ω={111,112,113,121,122,123,131,132,133,211,212,213,221,222,223,231,232,233,3 11,312,313,321,322,323,331,332,333} mocΩ=3³=27 Ze zbioru Ω usuwamy wszystkie wyniki nie spełniające kryteriów, zostaje: Ω'={123,213,222,231,321}

	5
P(A)=
	27

sajm: Pierwszy gracz rzuca kostką 4 ścienną z wartosciami 1 3 3 5, drugi gracz losuje przy pomocy ruletki z wartościami 0 2 2 6. Jakie prawdopodobieństwo na wygraną (wylosowanie większego numeru) ma każdy z graczy? Ω={10,12,12,16,30,32,32,36,30,32,32,36,50,52,52,56} mocΩ=16 Ω_P(A)={12,12,16,36,36,56} mocΩ_P(A)=6

	6
P(A)=
	16

	10
P(B)=
	16

PW: Co do ostatniego zadania (innych nie czytałem) to powiem, że zbaraniałem. Skąd taki "egzotyczny" model matematyczny − ta Ω={10,12,12,16,30,32,32,36,30,32,32,36,50,52,52,56}? Co oni robią z wynikami losowań i ile razy losują? Czegoś w treści zadania brakuje. Poza tym elementy zbioru muszą być rozróżnialne, nie może być w Ω jednakowych elementów 12 i 12, 32 i 32, 52 i 52. Co to jest A, a co B? Co oznacza napis "mocΩ_P(A)"?