Wektor na płaszczyźnie (bez układu współrzędnych) mysza00: Na płaszczyźnie dane są niewspółliniowe punkty A, B, C, D oraz dowolny punkt M. Wykaż, że jeśli MA−MB=MD−MC (nad każdym jest →, czyli wektor) , to czworokąt ABCD jest równoległobokiem.

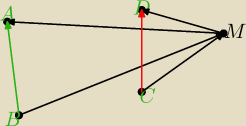
Marzena : → → → → Teza: MA−MB=MD−MC → → → → → 1.MA− MB =MA+(−MB)=BA (zielona linia) → → → → → 2. MD− MC = MD+(−MC)= CD (czerwony) → → Z tezy wynika, że BA=CD, a z tego wynika, że są również równoległe, więc jest to równoległobok. c.n.